Exercícios de Densidade de Cargas - Lista de Exercícios Resolvida
Questão 1
Observe a figura abaixo:
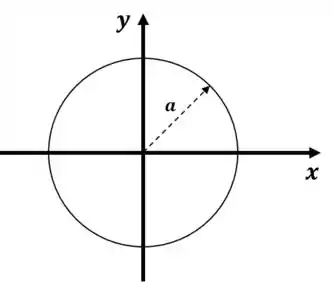
Dado que esse anel tem raio , digamos que a densidade de carga linear dele seja:
Onde é o ângulo trigonométrico, medido à partir do eixo no sentido anti-horário e é uma constante arbitrária. A questão é: qual a carga total do anel?
Ver solução completaQuestão 2
Um átomo de hidrogênio é constituído por um próton com carga e um elétron com carga . Podemos considerar o próton como uma carga puntiforme situada em , o centro do átomo. O movimento do elétron faz com que sua carga seja ‘espalhada’ ao longo de uma distribuição esférica em torno do próton, de modo que o elétron seja equivalente a uma carga por unidade de volume dada por
em que é chamado de raio de Bohr.
- Calcule a carga total do átomo de hidrogênio contida em uma esfera de raio centralizada sobre o próton;
- Como fica a carga quando ? Explique o resultado obtido nesse limite.
Questão 3
Uma esfera centrada na origem tem raio e a seguinte distribuição de cargas em seu volume:
Onde é uma constante negativa. Calcule a carga contida no interior de uma superfície esférica imaginária centrada na origem com raio , se:
Questão 4
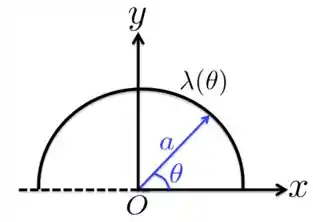
A Figura abaixo mostra uma semicircunferência de raio com uma carga positiva distribuída conforme a seguinte densidade linear , com sendo uma constante. Nessas circunstâncias, qual é a carga total da semicircunferência?
Questão 5
Uma barra não condutora possui comprimento e carga distribuída uniformemente. Quanto vale a densidade linear de carga dessa barra?
Ver solução completaQuestão 6
Um disco de raio de espessura desprezível tem um furo circular em seu centro. Dado que o raio do furo é e o disco possui densidade de carga superficial igual a:
Com tendo unidades de carga. Calcule a carga total do disco.
Ver solução completaQuestão 7
Dado um disco de raio com a seguinte distribuição de cargas superficiais:
Qual a carga total?
Ver solução completaQuestão 8
Seja uma esfera de raio e densidade de cargas dada pela expressão
Calcule a carga total na esfera.
Ver solução completaQuestão 9
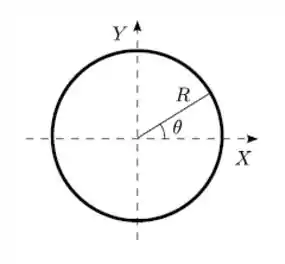
Um anel circular, fino, de raio , está disposto no plano , com centro na origem. Nele, há uma densidade linear de carga , onde é o tradicional ângulo polar e é uma constante. Qual é a carga total de tal anel?
- 0
Questão 10
Temos três distribuições não homogêneas de carga: I1) uma distribuição linear num fio de comprimento , cuja densidade linear de carga é: (); (2) Uma distribuição superficial sobre um disco de raio , cuja densidade superficial é: (); (3) Uma distribuição volumétrica numa esfera de raio , cuja densidade volumétrica é: (). Aqui, (, , ) são constantes. A carga total de cada uma dessas três distribuições é a mesma, . Qual das alternativas é a correta?
- ; ;
- ; ;
- ; ;
- ; ;
- ; ;
- ; ;
Questão 11
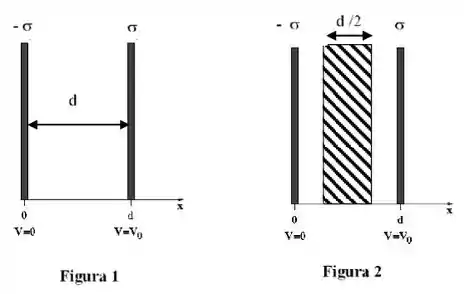
Duas placas isolantes muito grandes e de espessura desprezível são colocadas paralelamente uma em relação a outra, como mostrado na Figura 1. Na placa à direita, há uma distribuição superficial uniforme de cargas positiva. Na placa à esquerda, a distribuição de cargas é também uniforme, porém de densidade superficial igual e oposta à da direita. A distância entre as placas vale d e existe o vácuo entre as duas. Tomando a placa à esquerda (na posição ) como o referencial para o potencial mede-se que, sobre a placa à direita , o potencial tem valor.
a) Calcule a densidade superficial de cargas, , da placa isolante positiva em função de .
b) O sinal de é positivo ou negativo? Justifique.
Suponha agora que uma placa condutora neutra de espessura seja colocada na região entre as duas placas isolantes, como mostrado na Figura 2. Nesta nova configuração:
c) Calcule os valores do potencial em e faça um gráfico do potencial em função da distância para .
Questão 12
A velocidade de migração de elétrons em um fio condutor é , a densidade de elétrons é e a resistividade é . Nessas condições, quanto vale a intensidade do campo elétrico no condutor, em ? Se necessário use .
Ver solução completaQuestão 13
. Um anel circular de plástico, de raio , situa-se no plano com seu centro coincidente com a origem. O anel possui uma carga uniformemente distribuída ao longo da semicircunferência pertencente ao primeiro e segundo quadrantes e uma carga uniformemente distribuída o longo da semicircunferência pertencente ao terceiro e quarto quadrantes. Escolhendo o potencial elétrico como zero no infinito, quais valores melhor aproximam o potencial e o módulo do campo elétrico produzidos pelo anel em seu centro, respectivamente?
Dados: e .
Escolha uma opção:
e
e
e
e
e
e
e
e
Ver solução completaQuestão 14
Considere um bastão fino, retilíneo, situado no eixo , entre e .
Havendo uma densidade linear de carga , , em tal bastão, qual é a sua carga elétrica total?
.
.
.
.
.
Ver solução completaQuestão 15
11ª questão - O fio da figura está carregado com uma distribuição de carga não uniforme, de modo que sua densidade linear de carga depende da posição. Considerando-se os eixos da figura, cuja origem está no ponto , tem-se , sendo uma constante positiva. O campo elétrico no ponto , localizado no eixo que passa pelo centro do fio a uma distância deste, poderia ser representado por qual dos vetores abaixo?
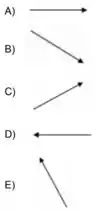
Questão 16
15ª questão - Uma esfera de borracha carregada homogeneamente com uma carga está na cavidade interior de uma esfera condutora oca. Os centros de ambas coincidem, como esquematizado ao lado. O gráfico abaixo mostra o módulo do campo elétrico da configuração ao longo de uma linha radial (os pontilhados servem apenas como referência). Sobre essa situação, indique a afirmativa FALSA:

A) Uma vez que o campo elétrico não se anula para , a esfera condutora deve estar carregada.
B) O raio da esfera de borracha é .
C) O raio interno da esfera condutora vale .
D) A carga da esfera de borracha em Coulombs é .
E) A superfície externa da esfera condutora possui uma densidade superficial de carga igual a .
Ver solução completaQuestão 17
Uma casca esférica condutora de raio interno e externo é carregada com uma carga . Além disso, uma carga pontual é colocada no centro da casca esférica.
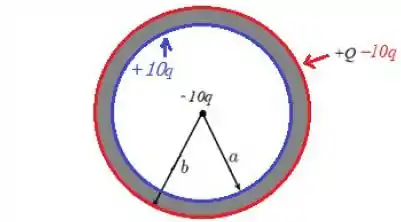
Qual é a densidade de carga na superfície externa da casca esférica?
Ver solução completa
Questão 18
A figura ao lado ilustra uma esfera oca condutora de raio interno e raio externo , que tem uma carga elétrica negativa . Uma carga pontual positiva é fixada no centro da esfera oca. Na figura, representa uma distância radial qualquer ao centro da esfera. Existe vácuo nas regiões e .
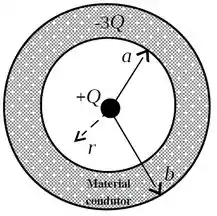
(a) Calcule o vetor campo elétrico (módulo, direção e sentido) em todos os pontos do espaço, ou seja, nas regiões (i) , (ii) e (iii) .
(b) Represente, em um desenho esquemático, um esboço das linhas de campo elétrico nas regiões , e .
(c) Determine a densidade superficial de carga na (i) superfície interna da esfera oca () e na (ii) superfície externa da esfera oca ().
Ver solução completaQuestão 19
6 - Uma esfera condutora oca tem raios de e , como mostrado na figura. A esfera carrega um excesso de carga . Uma carga pontual de está presente no centro da cavidade interna à esfera. A densidade de carga superficial na superfície esférica interna vale
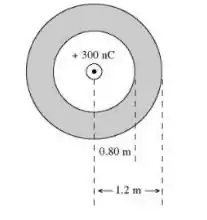
- Zero
Questão 20
Uma barra isolante fina, de comprimento , é posicionada sobre o eixo , de um sistema de coordenadas com o seu centro sobre a origem. Ela possui uma densidade linear de carga dada por , onde é uma constante positiva. Qual é a carga total dessa barra?
Questão 21
Considere um disco circular isolante de raio , que possui densidade superficial . Qual é a carga total desse disco?
Escolha uma:
Questão 22
Em um acelerador de partículas, dois feixes paralelos, um de prótons e outro de elétrons, possuem a mesma densidade volumétrica de partículas [número de partículas por volume]. Os prótons movem-se no sentido positivo do eixo , enquanto os elétrons no sentido oposto, ambos com velocidade de módulo . A intensidade da densidade de corrente no acelerador de partículas é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 23
Uma casca esférica condutora de raio interno e raio externo é carregada com uma carga liquida positiva . No interior da casca é posicionada uma pequena esfera condutora, de raio , carregada com a mesma carga Considere que no infinito e que
- Determine as expressões do potencial elétrico nas regiões:
- Se uma carga igual a é transportada do infinito até ser depositada na casca esférica, calcule (utilizando os valores fornecidos), nesta nova condição, quais são as densidades de carga superficiais na superfície da esfera de raio e nas superfícies internas e externas da casca esférica.
Questão 24
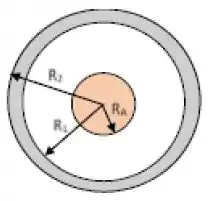
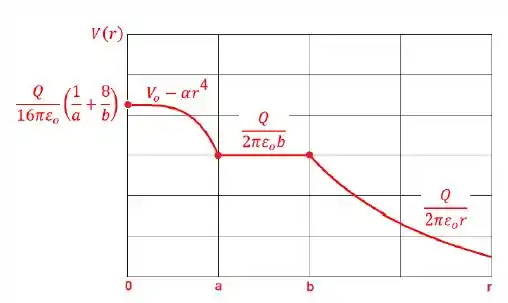
Um isolante esférico de raio a tem carga total Q (positiva) e está envolvido por uma casca esférica concêntrica de raios e , condutora em equilíbrio eletrostático. Não se sabe se a distribuição da carga no interior do isolante é uniforme ou não. A estrutura está imersa no vácuo (para O potencial elétrico em todos os pontos do espaço está caracterizado na Figura. Em particular, observam-se as dependências de V(r) com o raio r nos intervalos ; e que .
a) Após determinar o valor de em função de Q, a, b e (considerando que o potencial é uma função contínua de , obtenha expressões para o campo elétrico em todos os pontos do espaço).
b) Em seguida, determine as distribuições superficiais de carga (com sinais) nas superfícies interna (raio ) e externa (raio b) da casca condutora. Calcule a carga líquida da casca condutora, se houver.
Questão 25
Dois cilindros metálicos, concêntricos, infinitamente longos e de raios e atuam como placas de um capacitor cilíndrico. Considerando que há vácuo entre as placas, e que as placas interna e externa possuem densidade linear de carga e , respectivamente, calcule:
A diferença de potencial entre as placas.
Ver solução completaQuestão 26
11. (D) Uma casca isolante cilíndrica de raio e altura possui uma carga uniformemente distribuída sobre sua área.
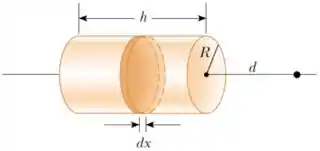
(a) Determine a densidade superficial de carga do cilindro.
Ver solução completaQuestão 27
3.10) Seja um capacitor de placas paralelas e circulares com raio e distância entre as placas
. Considere que há vácuo entre as placas, e que se estabeleça uma voltagem entre elas que
varia no tempo com a forma . Calcule:
(a) A densidade de corrente de deslocamento na região entre as placas.
Ver solução completa