Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Questões Conceituais - Ex. 4
O pequeno segmento de fio na FIGURA Q27.4 contém de carga.
a. O segmento é reduzido a um terço do comprimento original. Qual é a razão , onde e são as densidades de carga inicial e final, respectivamente?
b. Um próton está muito afastado do fio. Qual é a razão entre a intensidade da força elétrica sobre o próton após o segmento ter sido reduzido a um terço do comprimento original e a intensidade da força sobre o próton antes do segmento ter sido reduzido?
c. Suponha que o comprimento original do segmento de fio seja aumentado em 10 vezes. Que quantidade de carga deve ser adicionada ao fio para que a densidade linear de carga do mesmo não seja alterada?
Passo 1
Fala aí galerinha, blz??
Vamos para nossa quarta questão conceitual!
Em se tratando de corpos unidimensionais, como fios ou barras, nos quais a carga pode se distribuir ao longo de uma linha. Nessa situação, dizemos que temos uma densidade linear de cargas, que é “o quanto de carga você tem para cada unidade de comprimento do fio”.
Então, a gente precisa ver o quanto de carga existe em um pedacinho de fio , beleza?
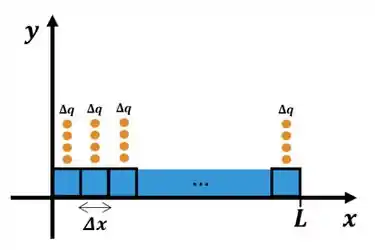
Note que, para o fio desenhado na figura, essa quantidade está igualmente distribuída por todo o fio, então dizemos que a barra está uniformemente carregada.
A unidade da densidade linear de cargas no S.I.é o “coulomb por metro”.
Como o fio está uniformemente carregado, então podemos também calcular o valor da densidade linear do fio como a divisão entre a carga total e o comprimento total do fio ;)
Assim, podemos pegar qualquer intervalinho do fio ou o fio inteiro para calcular a densidade linear uniforme de cargas.
Passo 2
a) Baseado nisso, pra essa primeira letra, dado o nosso raciocínio anterior, a razão entre as densidades final e inicial será igual a ...
Passo 3
b) Em seguida, temos que achar a razão entre a intensidade da força elétrica sobre o próton após o segmento ter sido reduzido a um terço do comprimento original e a intensidade da força sobre o próton antes do segmento ter sido reduzido...
Vamos então, usar a relação abaixo...
Dessa forma, se antes tínhamos , quando o fio foi reduzido a um terço do comprimento original teremos...
Passo 4
Assim, dada a fórmula da força eletrostática abaixo...
Sendo a distância entre as cargas, a carga do próton e a carga do fio, podemos achar a razão entre as forças antes e depois, quando o fio é reduzido a um terço do tamanho original...
Passo 5
c) Por fim, supondo que o comprimento original do segmento de fio seja aumentado em 10 vezes, precisamos encontrar a quantidade de carga que deve ser adicionada ao fio para que a densidade linear de carga do mesmo não seja alterada...
Para isso, vamos novamente recorrer à fórmula...
Assim, devemos acrescentar de carga ao fio para a densidade não ser alterada.
Pronto! Terminamos aqui!
Missão cumprida!
Resposta
a)
b)
c)