Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 97
Durante uma expansão isotérmica, um gás ideal a uma pressão inicial , se expande até que seu volume seja o dobro de seu volume inicial.
- Determine a pressão depois da expansão.
- O gás é, então, comprimido adiabática e quase estaticamente até que seu volume seja e sua pressão seja 1.32. O gás é monatômico, diatômico ou poliatômico?
- Como varia energia cinética de translação em cada estágio deste processo?
Passo 1
Legal galera, estamos trabalhando com uma expansão isotérmica. Para a letra a queremos saber a pressão final.
O que sabemos?
Sabemos que,
Também sabemos o volume final, certo?
Como se trata de um gás ideal, podemos usar:
Como estamos em um processo isotérmico, nRT é constante, tanto para o estado inicial quanto final:
Se queremos saber bora isolá-la:
Substituindo
Ou seja:
A letra a foi tranquila, não foi? Bora pra b !!
Passo 2
Antes de tudo vamos desenhar o que está acontecendo:
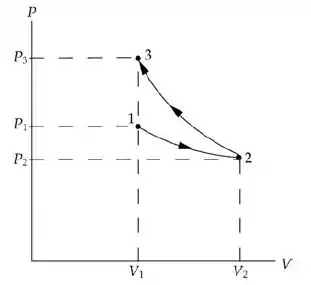
Sabemos que:
E:
E o ponto final:
Como está ocorrendo uma compressão adiabática podemos usar a relação entre pressão e volume existente:
Não sabemos se o gás é monoatômico, diatômico ou poliatômico, então ainda não sabemos Vamos deixa-lo quieto por um tempo e substituir os demais:
Com a nossa incógnita no expoente, fica difícil trabalhar! Vamos tirá-lo:
Pelas propriedades do ln:
Sabemos que:
Se temos 5 graus de liberdade, estamos lidando com um gás diatômico.
FInalizandoo..
Passo 3
A letra c é bem teórica, durante o primeiro processo a temperatura não varia. Se não há variação da temperatura, também não há variação da energia cinética. Quando o processo é adiabático, a energia cinética translacional vai variar porque a temperatura varia.
Para saber em quanto vamos usar uma relação para o caso adiabático:
Substituindo:
Então, a energia cinética vai aumentar em um fator de 1,32.
Resposta
- ;