Um elétron é acelerado a partir do repouso por uma diferença de potencial e penetra em uma região onde existe um campo magnético uniforme, na qual descreve um movimento circular uniforme. A Fig. 28-37 mostra o raio da circunferência descrita pelo elétron em função de . A escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . Qual é o módulo do campo magnético?
Passo 1
Fala aí! Tudo certinho? 😬

Nesse problema temos um elétron que é acelerado por um potencial e passa a sofrer efeito de um campo magnético descrevendo um movimento circular. Com base nos dados descritos no enunciado, queremos determinar o modulo do campo magnético que age sobre o eletron.
Tem ideia de como fazemos isso? 😉
Passo 2
Primeiramente, vamos escrever a lei de conservação de energia:
Agora, vamos escrever a equação para o raio da trajetória circular, e substituir a velocidade:
Portanto, podemos utilizar a inclinação do gráfico para calcular o coeficiente multiplicando .
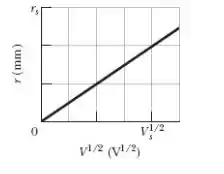
Pegando os pontos , com . E , com , temos:
Agora, podemos colocar B em evidência:
E aí, entendeu tudo? Responde Aí! 🤔
