Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.6 - Ex. 31

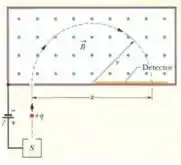
Um espectrômetro de massa (Fig. 28-12) é usado para separar íons de urânio de massa 3,92 × 10 - 25 k g e carga 3,20 × 10 - 19 C de íons semelhantes. Os íons são submetidos a uma diferença de potencial de 100   k V e depois a um campo magnético uniforme que os faz descrever um arco de circunferência com 1,00   m e raio. Após sofrerem um desvio de 180 ° e passarem por uma fenda com 1,00   m m de largura e 1,00   c m de altura, são recolhidos em um reservatório. (a) Qual é o módulo do campo magnético (perpendicular) do separador? Se o aparelho é usado para separar 100   m g de material por hora, calcule (b) a corrente dos íons selecionados pelo aparelho e (c) a energia térmica produzida no reservatório em 1,00   h .

Passo 1

E aí, pessoal! 😁

Temos íons de urânio, com massa m = 3,92 �� 10 - 25 k g submetidos a uma DDP de V = 100 k V e depois a um campo magnético que os faz ter uma trajetória circular de raio R = 1,00 m . Depois de percorrer meia circunferência, passam por uma fenda de 1,00 mm de largura e 1,00 cm de altura e são recolhidos em um reservatório. O esquema é semelhante ao da figura 28-12:

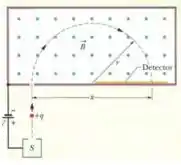
Para calcular o campo magnético, vamos utilizar a seguinte relação para o raio:

r = 1 B 2 m V q

Veja só! 😉

Passo 2

Colocando o campo em evidência:

B = 1 r 2 m V q

B = 1 1,0 2 3,92 × 10 - 25 100 × 10 3 3,20 × 10 - 19 = 0,495 T

(b) Temos que a massa de íons separados por segundo é:

M = 100 × 10 - 6 k g 3600 = 2,78 × 10 - 8 k g / s

Dessa forma, o número de íons separados por segundo é a massa de íons por segundo dividido pela massa de um íon:

N = M m

N = 2,78 × 10 - 8 3,92 × 10 - 25 = 7,09 × 10 16 s - 1

Por definição a corrente é o número de partículas vezes a sua massa.

i = q N

i = 3,20 × 10 - 19 7,09 × 10 16 = 2,27 × 10 - 2 A

Tranquilo até aqui? 😎

Passo 3

(c) Como cada íon deposita uma energia certa energia no reservatório, a energia depositada em uma hora é a quantidade de energia depositada por uma partícula, q V , multiplicado pelo número de partículas que chegam em uma hora, N Δ t :

E = q V N Δ t

E = 3,20 × 10 - 19 100 × 10 3 7,09 × 10 16 3600

E = 8,17 × 10 6 J

E aí! entendeu tudo? Responde Aí!

Resposta

(a) B = 495 m T (b) i = 22,7 m A

(c) E = 8,17 M J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que, em um condutor submetido a um campo elétrico E → e a um campo magnético tal que ω C τ = 1 , a densidade de corrente j → faz um ângulo de 45 ° com o campo elétrico.
Um anel com raio de 10c m conduz uma corrente de 20A . (a) Calcule o dipolo magnético do anel. Calcule o torque exercido sobre o anel por um campo magnético de 1000G com orientação (b) paralela ao eix
Calcule a intensidade da força realizada por um campo magnético de 1,0T sobre um fio com 1,0m de comprimento ortogonal ao campo, conduzindo uma corrente de 1,0A .
a) Calcule o valor da corrente elétrica que, ao circular a Terra em um anel sobre sua superfície, iria gerar um dipolo elétrico igual ao do planeta.b) Faça o mesmo para uma estrela de nêutrons cujo ra
Um gás de elétrons está em regime de efeito Hall quântico fracionário. Calcule a resistência Hall quando o sistema está em um patamar de R H correspondente aos números quânticos p = 1 e n = 3 .