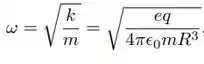Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 24.Exercícios e Problemas - Ex. 30
Um elétron tem seu movimento restrito ao eixo central do anel de carga de raio R discutido na Seção 24-6. Mostre que a força eletrostática exercida sobre o elétron pode fazê-lo oscilar através do centro do anel com uma frequência angular de
Onde q é a carga do anel e m é a massa do elétron.
Passo 1
E aí galerinha do bem, galerinha do mal e galerinha que gosta de uva passa na comida, vem comigo, pois como o livro explica a magnitude do campo elétrico num ponto localizado sobre o eixo de um anel homogeneamente carregado, a uma distância z do centro do anel, é dado por:
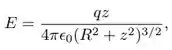
onde q é a carga sobre o anel e R é o raio do anel.
Passo 2
Para que possa haver oscilação a carga q sobre o anel deve ser necessariamente positiva. Para uma carga q positiva, o campo aponta para cima na parte superior do anel e para baixo na parte inferior do anel. Se tomarmos a direção para cima como sendo a direção positiva, então a força que atua num elétron sobre o eixo do anel é dada por:
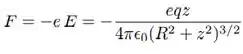
onde e representa a magnitude da carga do elétron.
Passo 3
Para oscilações de pequena amplitude, para as quais vale , podemos desprezar z no denominador da expressão da força, obtendo então, nesta aproximação:
Desta expressão reconhecemos ser a força sobre o elétron uma força restauradora: ela puxa o elétron em direção ao ponto de equilíbrio z = 0. Além disto, a magnitude da força é proporcional a z, com uma constante de proporcionalidade como se o eletron estivesse conectado a uma mola.
Passo 4
Ao longo do eixo, portanto, o elétron move-se num movimento harmônico simples, com uma frequência angular dada por:
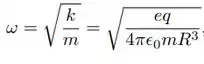
onde m representa a massa do elétron.
Resposta
Por fim podemos confirmar que:
