Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 66

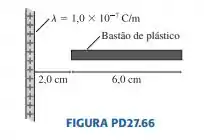
Suponha que uma de suas atribuições como físico seja desenvolver uma maneira de usar a eletricidade para lançar um pequeno bastão de plástico com 6,0   c m de comprimento. Você, então, decide eletrizar o pequeno bastão friccionando-o com um pano e, depois, mantê-lo próximo a um fio longo que fora previamente carregado. Quando você solta o bastão, a força elétrica exercida pelo fio o arremessará para longe. Suponha que você consiga carregar uniformemente o bastão com 10   n C e que a densidade linear de carga do fio longo seja de 1,0 ×   10 - 7 C m . Qual é a intensidade da força elétrica sobre bastão de plástico se sua extremidade mais próxima ao fio está a 2,0   c m de distância?

Passo 1

Faaaaaala, galera... Tranquileba??

Primeiro precisamos definir o campo elétrico em um bastão, então:

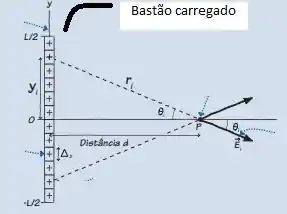
Vemos que as componentes em y se cancelam, sobrando somente em x, de forma que:

E b a s t ã o = E i x cos ⁡ θ

Sabemos que o campo elétrico é dado por:

d E = 1 4 π ϵ 0   d Q r 2  

Assim:

d E b a s t ã o = 1 4 π ϵ 0   d Q r 2 cos ⁡ θ

Pela imagem, vemos que:

cos ⁡ θ = d R

E que:

R = y 2 + d 2

Assim:

cos ⁡ θ = d y 2 + d 2

E ficando:

d E b a s t ã o = 1 4 π ϵ 0   d Q y 2 + d 2 d y 2 + d 2  

d E b a s t ã o = 1 4 π ϵ 0   d   d Q y 2 + d 2 3 2  

E sabemos que a densidade linear de carga é:

λ = Q L

Logo:

Q = λ L → d Q = λ d L

Vemos na imagem que d L = d y

Assim ficamos com:

d E b a s t ã o = 1 4 π ϵ 0   d * λ   d y y 2 + d 2 3 2  

Integrando sabendo que - L 2 ≤ y ≤ + L 2  

E b a s t ã o = λ d 4 π ϵ 0 ∫ - L 2 L 2 d y y 2 + d 2 3 2

E b a s t ã o = λ d 4 π ϵ 0 ∫ - L 2 L 2 d y d 2 y d 2 + 1 3 2

E b a s t ã o = λ d 4 π ϵ 0 ∫ - L 2 L 2 d y d 3 y d 2 + 1 3 2

Façamos:

y d = tan ⁡ θ

Logo:

d y = d  sec 2 ⁡ θ   d θ

E quando:

y = L 2 → θ = tan - 1 ⁡ L 2 d

E:

y = - L 2 → θ = tan - 1 ⁡ - L 2 d

Assim ficando:

E b a s t ã o = λ d 4 π ϵ 0 ∫ tan - 1 ⁡ - L 2 d tan - 1 ⁡ L 2 d d  sec 2 ⁡ θ   d θ d 3 tan 2 ⁡ θ + 1 3 2

E b a s t ã o = λ 4 π ϵ 0 1 d ∫ tan - 1 ⁡ - L 2 d tan - 1 ⁡ L 2 d   sec 2 ⁡ θ   d θ tan 2 ⁡ θ + 1 3 2

Sabemos que:

tan 2 ⁡ θ + 1 = sec 2 ⁡ θ

E b a s t ã o = λ 4 π ϵ 0 1 d ∫ tan - 1 ⁡ - L 2 d tan - 1 ⁡ L 2 d   sec 2 ⁡ θ   d θ sec 3 ⁡ θ

E b a s t ã o = λ 4 π ϵ 0 1 d ∫ tan - 1 ⁡ - L 2 d tan - 1 ⁡ L 2 d cos ⁡ θ   d θ

E b a s t ã o = λ 4 π ϵ 0 1 d s e n   θ - L 2 d l 2 d

E b a s t ã o = λ 4 π ϵ 0 1 d 2 L L 2 + 4 d 2

E b a s t ã o = λ 4 π ϵ 0 1 d 2 L 2 L 2 2 + d 2

E b a s t ã o = λ 4 π ϵ 0 1 d L L 2 2 + d 2

Sabemos que:

λ = Q L

∴ E b a s t ã o = 1 4 π ϵ 0 1 d Q L 2 2 + d 2

Agora, façamos esse bastão ser infinito, ou seja, L → ∞

E f i o   i n f i n i t o = 1 4 π ϵ 0 1 d Q L 2 ( 1 2 2 + d L 2

E f i o   i n f i n i t o = 1 4 π ϵ 0 1 d Q L 2

Sabemos que:

λ = Q L

∴ E f i o   i n f i n i t o = 1 4 π ϵ 0   2 λ d

Passo 2

Assim:

d F = E   d q

Sabemos que:

λ ' = q L

d q = λ ' d L

Consideremos d L = d x , pelo comprimento do bastão de plástico estar no eixo x. E λ ' é a densidade de carga linear do bastão de plástico e λ do fio. E a distância d que queremos tomar é x, que é a distancia do fio até o bastão de plástico.

Assim:

d F = 1 4 π ϵ 0   2 λ x λ ' d x

Passo 3

Assim integrando em todo o comprimento do bastão de plástico:

F = 2 λ   λ ' 4 π ϵ 0 ∫ 2 × 10 - 2   m 8 × 10 - 2 m d x x

F = 2 λ   λ ' 4 π ϵ 0   ln ⁡ x 2 × 10 - 2 m 8 × 10 - 2     m

F = 2 λ   λ ' 4 π ϵ 0   ln ⁡ 8 × 10 - 2 m 2 × 10 - 2   m

F = 2 λ   λ ' 4 π ϵ 0   ln ⁡ 4

F = 2 λ   q l b a s t .   p l a s t i c o 4 π ϵ 0   ln ⁡ 4

Colocando valores:

F = 9 × 10 9 N m 2 C 2 2 1,0 ×   10 - 7 C m 10 × 10 - 9   C 6 × 10 - 2 m ln ⁡ 4

∴ F = 4.2 × 10 - 4 N

Resposta

∴ F = 4.2 × 10 - 4 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 22-52, uma barra não condutora "semi-infinita" (ou seja, infinita apenas em um sentido) possui uma densidade linear de cargas uniforme λ . Mostre que o campo elétrico E → p no ponto P faz um â
Dois planos paralelos estão uniformemente carregados, com densidades de cara σ e - σ , respectivamente. Calcule o campo elétrico em pontos acima de ambos, abaixo de ambos, e entre os dois. Represente
Uma carga puntiforme q é colocada numa caixa cúbica de aresta l . Calcule o fluxo do campo elétrico sobre cada uma das faces se a carga ocupa o centro do cubo.
Na Fig. 24-37, uma barra não-condutora, de comprimento L, tem uma carga -q uniformemente distribuída ao longo de seu comprimento. (a) Qual a densidade linear de carga da barra? (b) Qual o campo elétri
Uma barra fina de vidro e encurvada na forma de um semicírculo de raio r. Uma carga +Q está distribuída uniformemente ao longo da metade superior, e uma carga −Q, distribuída uniformemente ao longo da