Mostre que uma linha de carga infinita, com densidade linear de carga , exerce sobre um dipolo elétrico uma força atrativa de intensidade . Considere que r seja muito maior do que a separação entre as cargas do dipolo.

Faaaaaala, galera... Tranquileba??

Sabemos que:

Então precisamos saber o campo elétrico que, neste caso, uma linha de carga infinita exerce a um ponto com a uma distancia d. Vamos lá acha-lo?!

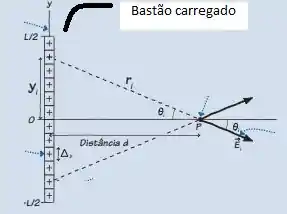
Vemos que as componentes em y se cancelam, sobrando somente em x, de forma que:

Sabemos que o campo elétrico é dado por:

Assim:

Pela imagem, vemos que:

E que:

Assim:

E ficando:

E sabemos que a densidade linear de carga é:

Logo:

Vemos na imagem que

Assim ficamos com:

Integrando sabendo que

Façamos:

Logo:

E quando:

E:

Assim ficando:

Sabemos que:

Sabemos que:

Agora, façamos esse bastão ser infinito, ou seja,

Sabemos que:

Essa doeu até a mão ☹. Mas chegamos!!

Assim: