Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 44
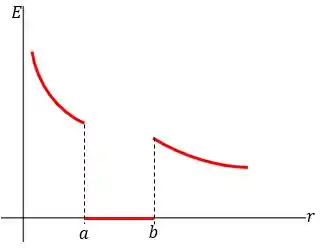
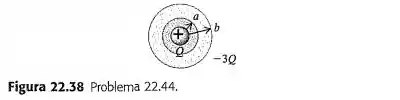
Uma esfera oca condutora com raio interno e raio externo possui uma carga puntiforme positiva , localizada em seu centro. A carga total sobre a esfera oca é igual a e está isolada de suas vizinhanças (Figura ). Deduza uma expressão para o módulo do campo elétrico em função da distância ao centro para as regiões , , e . Qual é a densidade superficial de carga sobre a superfície interna da esfera oca condutora? Qual é a densidade superficial de carga sobre a superfície externa da esfera oca? Faça um desenho indicando as linhas de campo elétrico e a localização de todas as carga. Faça um gráfico do módulo do campo elétrico em função da distância .
Passo 1
Para saber o campo elétrico em cada situação, precisamos considerar uma superfície gaussiana adequada para cada uma delas.
Primeiramente, supondo uma superfície gaussiana esférica de raio , ela envolve a carga da esfera central . Logo, o seu campo elétrico será dado por:
Já para uma superfície gaussiana que tenha raio , visto que nessa região ela se encontra no interior da esfera oca que é um condutor sólido carregado, então o seu campo elétrico é nulo.
Agora para a superfície gaussiana de raio , ela envolve a carga central e a carga mais externa de valor . Como a carga líquida é dada por no interior da superfície de Gauss, então o seu campo elétrico na superfície externa será dado por:
Passo 2
Na região da superfície interna da esfera oca, ou seja, em , por se tratar de um condutor carregado, o campo elétrico deve ser nulo.
Como a superfície gaussiana nesta região envolve a carga do centro, então a carga na superfície interna deve ser . Consequentemente, essa superfície possui densidade superficial de carga:
Passo 3
Agora, como a esfera oca possui carga total igual a , tendo uma carga na superfície interna, a carga na superfície externa (em ) deve ser para resultar na carga total. Logo, a superfície externa tem densidade superficial de carga com o seguinte valor:
Passo 4
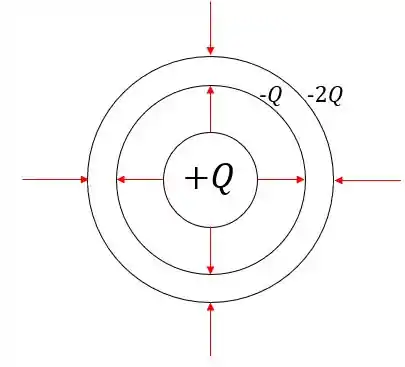
O esboço das linhas do campo elétrico e dos sinais das cargas é dado a seguir:
Passo 5
Por fim, o gráfico desse caso é dado por:
