Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 40
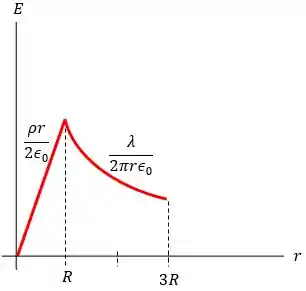
Um cilindro sólido muito longo de raio possui uma distribuição uniforme de carga positiva, sendo a carga por unidade de volume. Deduza uma expressão para o campo elétrico no interior do volume, a uma distância do eixo do cilindro, em termos da densidade de carga . Qual é o campo elétrico em um ponto fora do volume, em termos da carga por unidade de comprimento do cilindro? Compare os resultados dos itens e para . Faça um gráfico do módulo do campo elétrico em função da distância , de até .
Passo 1
Supondo uma superfície gaussiana cilíndrica de raio e comprimento com o mesmo eixo que o cilindro, temos que o seu campo elétrico será dado através da carga por unidade de volume. Então, usando a equação do campo elétrico para uma linha infinita, teremos:
Onde a área é dada por:
E a carga é dada através da densidade de carga:
Portanto, o campo elétrico será dada por:
Com sentido para fora, pela carga ser positiva.
Passo 2
Agora, consideramos uma superfície gaussiana cilíndrica com raio e comprimento , ela terá uma densidade de carga por unidade de volume:
Tal que, deixando a densidade volumétrica em função da densidade linear:
Então, nesse caso, o campo elétrico será calculado por:
Com sentido para fora.
Passo 3
Se , então para o primeiro caso, o capo elétrico será:
E para o segundo caso:
Assim, ambos os campos elétricos são iguais e, logo, elas coincidem.
Passo 4
O gráfico que mostra esses resultados está mostrado a seguir:
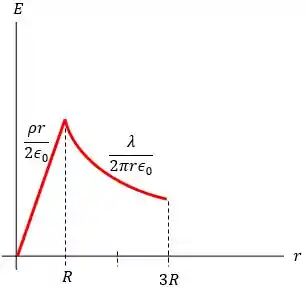
Resposta
