Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Problemas - Ex. 65
Uma espira retangular com largura e um fio deslizante com massa estão como indica a figura 29.53. Um campo magnético uniforme está orientado perpendicularmente ao plano da espira para dentro do plano da figura. O fio deslizante recebe uma velocidade escalar inicial e, a seguir, é libertado. Não há atrito entre o fio deslizante e a espira, e a resistência da espira é desprezível em comparação à resistência do fio.
Obtenha uma expressão para , o módulo da força exercida sobre o fio enquanto ele se move a uma velocidade escalar .
Mostre que a distância que o fio percorre antes de atingir o repouso é .
Passo 1
A partir da imagem podemos indicar as forças que agem sobre a nossa haste em movimento. Assim, temos
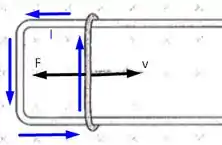
Para encontrarmos o que procuramos vamos usar a lei de Faraday para calcular a fem induzida e a lei de ohm para calcular . Devemos lembrar que quando o fio se move com velocidade a fem induzida é
E a corrente induzida será
A corrente induzida flui para cima no fio, como mostrado na figura acima, então a força exercida pelo campo magnético na corrente induzida é para a esquerda. se opõe ao movimento do fio, isso se deve a lei de Lenz. Sendo assim, a magnitude da força será dada por
Passo 2
Agora, para demonstrarmos a expressão dada no enunciado vamos começar aplicando a segunda lei de Newton onde teremos
Onde poderemos encontrar
Lembrando-se que temos
Integrando ambos os lados vamos encontrar
Agora, precisamos reparar que quando então . Dessa forma, resolvendo para vamos encontrar
No repouso temos e isso acontece quando . Então vamos ter
Resposta