Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 15.Exercícios e Problemas - Ex. 17
Uma esfera de raio tem uma carga uniformemente distribuída em seu volume. Utilize a lei de Gauss e considerações de simetria para calcular o campo elétrico à distância do centra da esfera, (a) para e (b) para .
Passo 1
Esse é um dos exercícios mais tradicionais sobre lei de Gauss! Temos uma esfera uniformemente carregada com carga , de modo que sua densidade volumétrica de carga será
A lei de Gauss estabelece que a integral de fluxo do campo elétrico cobre uma superfície fechada deve ser proporcional a carga contida dentro do volume limitado pela superfície:
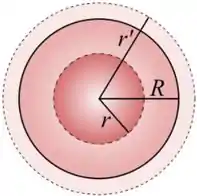
Para esse problema, vamos considerar duas superfícies gaussianas esféricas, uma com raio e outra com raio :
Por simetria, o campo elétrico deve ser radial, de forma que
Como o campo deve depender apenas da distância , ele sai da integral:
Com isso, a lei de Gauss nos dá a relação:
Passo 2
Vamos resolver primeiro o item (b) que é mais simples. Para pontos fora da esfera de raio , isto é, para , a carga contida dentro da superfície gaussiana de raio é toda a carga da esfera, de modo que
Assim,
Portanto, para :
Nessa situação, é como se toda a carga estivesse concentrada no centro da esfera!
Passo 3
Agora vamos para o item (a) com . Como nesse caso a esfera de raio não envolve toda a esfera de raio , temos que considerar apenas a carga contida dentro dela, que será a densidade vezes o volume dela:
Usando a expressão para que achamos no passo 1:
Repare que essa carga depende de , o que faz sentido né? Quanto maior o raio maior será a carga envolvida 😉.
Daí, a lei de Gauss nos dá
Logo, para :
É legal perceber que as duas fórmulas dão o mesmo valor para , de modo que o campo elétrico é contínuo nesse problema: ele cresce linearmente com o raio para e depois cai com o quadrado do raio para .