Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 43

Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para r < R , onde B é uma constante e ρ = 0 para r > R . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elétrico no interior e no exterior da distribuição de cargas. (c) Represente a magnitude do campo elétrico como uma função da distância r a ao centro da esfera.

Passo 1

Fala ai, gente. Tudo tranquilo? Bom, aqui nesse exercício a gente está querendo calcular a carga total e o campo elétrico no interior de uma esfera isolante que possui uma densidade de carga não constante. Vamos proceder como no exercício anterior, blz?

Passo 2

  1. No exercício anterior, a gente tinha chego na expressão:

    2. q = ∫ ρ   4 π r 2   d r

    Usando o valor de ρ dado, temos

    q = 4 π B ∫ 0 R r   d r = 2 π B R 2

    Passo 3

  2. Vamos calcular o campo elétrico nas duas situações dada:
  • Para r < R , temos que a carga interna é q i n t = 2 π B r 2 . Sendo assim,

    • ∮ E   d A = q i n t ε 0 E 4 π r 2 = 2 π B r 2 ε 0 E = B 2 ε 0

    Veja que E é constante no interior da esfera.

  • Para r > R , temos que a carga interna é q i n t = 2 π B R 2 . Logo,

∮ E   d A = q i n t ε 0 E 4 π r 2 = 2 π B R 2 ε 0 E = B R 2 2 ε 0 r 2

Passo 3

  • Basta construir o gráfico de E versus r . Veja:

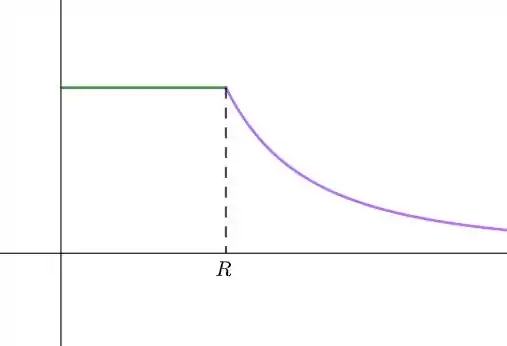
    • Note, como no exercício anterior, que o campo elétrico E é contínuo em um isolante ;)

    Resposta

    1. 2 π B R 2
    2. B / 2 ε 0
    3. B R 2 / ε 0 r 2
    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    PROTEÇÃO CONTRA RADIAÇÃO CÓSMICA. Um dos perigos para os seres humanos no espaço é a radiação cósmica: partículas carregadas com alta energia emitidas pelo Sol. Durante uma erupção solar, a intensidad
    PROTEÇÃO CONTRA RADIAÇÃO CÓSMICA. Um dos perigos para os seres humanos no espaço é a radiação cósmica: partículas carregadas com alta energia emitidas pelo Sol. Durante uma erupção solar, a intensidad
    59 . Em um experimento, o campo elétrico é medido em pontos a distâncias r de um fio retilíneo uniformemente carregado, que possui carga por unidade de comprimento λ e comprimento l , em que l ≫ r . E
    O fluxo elétrico resultante através de uma superfície fechada é - 1000N m 2 C . Que quantidade de carga está encerrada pela superfície?
    Qual é o fluxo elétrico resultante através do cilindro da FIGURA EX28.21?