Uma fina casca esférica não-condutora de raio tem carga total uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio , coaxial com a primeira, tem carga uniformemente distribuída em sua superfície. (a) Use a lei de Gauss para obter expressões para o campo elétrica em cada uma das três regiões: , e . (b) Qual deveria ser a razão entre as cargas e os sinais relativos para e para que o campo elétrico fosse zero na região ? (c) Represente as linhas de campo elétrico para a situação da parte (b) quando é positiva?
Passo 1
Fala, beleza? Então, esse exercício quer que a gente calcule, a partir da lei de Gauss, o campo elétrico para situações esfericamente simétricas. Nesse tipo de situação, nada melhor do que tomar a nossa superfície gaussiana como sendo uma esfera concêntrica com as demais e de raio .
Passo 2
- Para , temos
- Para :
- Para , temos
- Notemos que para , bastará que , ou seja, . Assim, o sinal relativo entre e são opostos.
- Nesse caso, só haverá campo elétrico entre as esferas. Assim, temos algo do tipo:
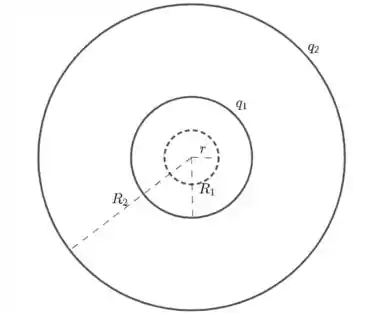
Dessa forma temos que
Porém, no interior da esfera de raio , a carga interna é nula; . Assim, o lado direito da equação acima é nulo. A única forma do lado esquerdo também ser nulo é .
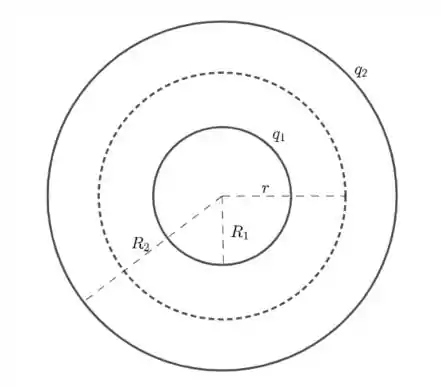
Temos que
Nesse caso, . Como
segue que
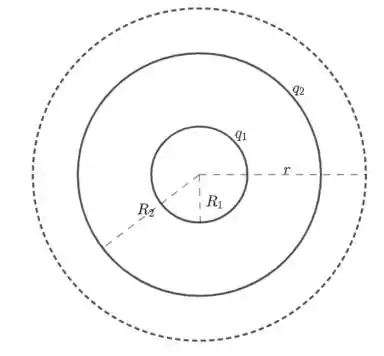
Temos que
Como
Seque
Passo 3
Passo 4
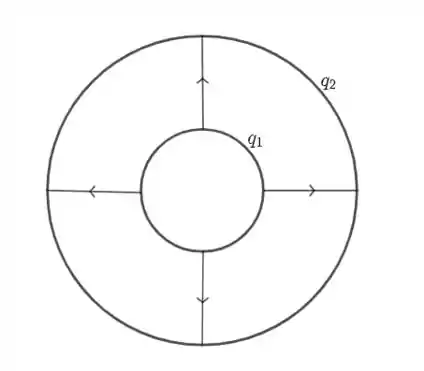
Resposta
- Para , .
- Para ,
- Para ,
- Ver imagem.
Resposta
Ei, a resposta está no passo a passo :)