Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 28
Três capacitores estão conectados em um triângulo, como mostra a Figura 24-35. Determine uma expressão para a capacitância equivalente entre os pontos e em termos dos três valores de capacitância.
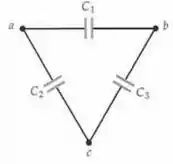
Passo 1
Cara... Queremos aqui determinar a capacitância equivalente vista pelo terminal ...
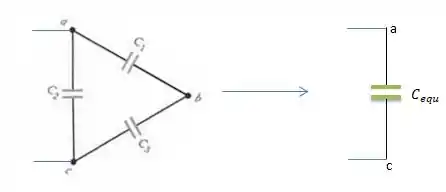
Mas repare que os capacitores e estão em série cum com o outro, e o conjunto está em paralelo com o capacitor . Para ficar mais fácil, vamos remontar o circuito para...
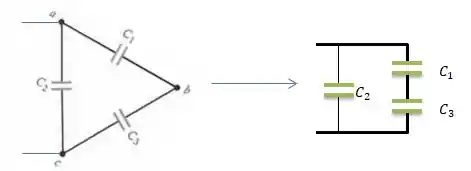
Viu só? Bem mais fácil de ver, neh?
Repare que antes de determinar a capacitância equivalente que é o nosso objetivo... Temos que passar por um passo que é determinar qual é a equivalência da junção série de e (vou chamar de )...
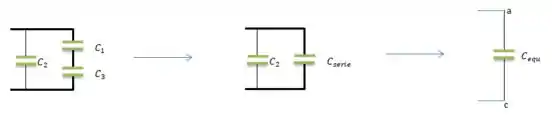
Passo 2
Para encontrar a , basta se lembrar de que capacitores em série possuem capacitância equivalente () através da fórmula...
Então...
Passo 3
Beleza, agora que já passamos por esse passo interno, podemos determinar o que queremos no exercício que é o ...
Fazendo então o paralelo entre e . Em paralelo, a resultante pode ser dada pela soma...
Então...
Então essa vai ser a capacitância equivalente vista pelos terminais do capacitor, ta ligado?