Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 110
Uma estrada na direção leste passa por uma pequena colina. Você dirige um carro com massa a uma velocidade constante sobre o topo da colina, onde a forma da rodovia é bem próxima do arco de um círculo com raio . Foram colocados sensores na superfície da estrada para medir a força para baixo que os carros exercem sobre a superfície em diversas velocidades. A tabela mostra os valores dessa força versus a velocidade do seu carro:
Trate o carro como uma partícula. (a) Represente os valores graficamente de modo que se ajustem a uma linha reta. Você pode ter de elevar a velocidade, a força ou ambos à mesma potência. (b) Use o gráfico do item (a) para calcular e . (c) Que velocidade máxima o carro poderá ter no topo da colina e ainda não perder contanto com o solo?
Passo 1
Fala pessoal, esse é um problema bem legal em que vamos fazer um ajuste gráfico de um conjunto de dados!
O primeiro passo em qualquer problema desse tipo é entender o que realmente está acontecendo e obter um modelo. Considerando que o carro está no topo da pista, a fora peso aponta para baixo (dentro da trajetória circular) e a força normal para cima (fora da trajetória circular), de modo que
Como , segue que
Isolando :
Com isso, devemos fazer o gráfico de em função de , de modo que
Passo 2
A seguir escrevo a tabela com e :
Fazendo um plot desses pontos, encontramos
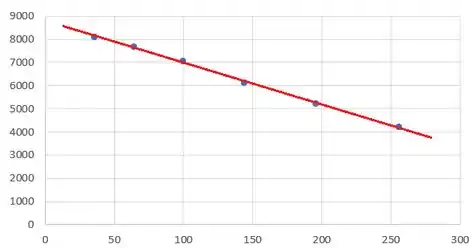
Isso resolve o item (a)! Observe que os dados se alinham bem, concordando com o modelo!
Passo 3
O próximo passo é encontrar os valores de e . Para isso, escolhemos dois pontos da reta:
Eu escolhi os dois pontos mais extremos para ter uma boa representação da reta. O ideal seria fazer um ajusta via método dos mínimos quadrados usando um software, mas para os propósitos dessa questão vamos usar esse método mais rudimentar...
Substituindo na equação :
Resolvendo esse sistema você acha:
Com isso, temos
Como , segue que
Da mesma forma,
Passo 4
A velocidade máxima ocorre para , de modo que
Portanto,
Assim,