Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.Problemas - Ex. 92

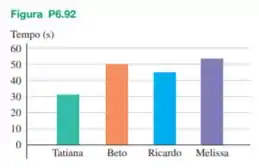
Para um experimento no laboratório de física, quatro colegas sobem as escadas do porão até o último andar do seu prédio — uma distância vertical de 16,0   m . Os colegas e suas massas são: Tatiana, 50,2   k g ; Beto, 68,2   k g ; Ricardo, 81,8   k g e Melissa, 59,1   k g . O tempo gasto por cada um deles aparece na Figura P6.92. (a) Considerando apenas o trabalho realizado contra a gravidade, qual deles obteve a maior potência de saída média? E a menor? (b) Chang está em boa condição física e possui massa de 62,3   k g . Se a sua potência de saída média é 1,00   h p , quantos segundos seriam necessários para ele subir pelas escadas?

Passo 1

Fala galerinha, beleza?

Para calcular a potência de cada um, temos que dividir o trabalho realizado para vencer o peso ( m g h ) pelo tempo:

P = m g h Δ t

Para Tatiana, temos

P T a t i a n a = 50,2 ⋅ 9,8 ⋅ 16,0 31 = 253,9   W

Para os demais:

P B e t o = 68 , 2 ⋅ 9,8 ⋅ 16,0 50 = 213,8   W

P R i c a r d o = 81,8 ⋅ 9,8 ⋅ 16,0 45 = 285   W

P M e l i s s a = 5 9,1 ⋅ 9,8 ⋅ 16,0 52 = 178,2   W

Comparando as potências, vemos que a maior pertence ao Ricardo e a menor é a da Melissa.

Passo 2

No item (b), queremos achar o tempo:

Δ t = m g h P

A potência foi fornecida em cavalos ( h p ). Precisamos convertê-la para watts usando 1   h p = 745,7   W . Portanto,

Δ t = 62,3 ⋅ 9,8 ⋅ 16,0 745,7

Com isso, achamos

Δ t = 13,1   s

Resposta

m a i o r → R i c a r d o

m e n o r → M e l i s s a

Δ t = 13 , 1   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Conforme um motorista pisa no acelerador, um carro de massa 1160k g acelera do repouso. Durante os primeiros segundos do movimento, a aceleração do carro aumenta com o tempo de acordo com a expressão
Uma turbina de vento em um parque eólico gira em resposta a uma força de resistência do ar de alta velocidade, R= 1 2D ρ A v 2 . A potência disponível é P=R v= 1 2D ρ π r 2 v 3 , em que v é a velocida
A massa de um carro é 1500k g . O formato da carroceria é tal que o coeficiente de arrasto aerodinâmico é D=0,330 e a área frontal é 2,50m 2 . Supondo que a força de arrasto seja proporcional a v 2 e
Durante uma corrida, uma pessoa transforma cerca de 0,600J de energia química em mecânica por passo por quilograma de massa corporal. Se um corredor de 60,0k g transforma energia a uma taxa de 70,0W d
Uma partícula de 4,00k g se move ao longo do eixo x . Sua posição varia no tempo, de acordo com x=t+2,0 t 3 , em que x está em metros e t em segundos. Encontre (a) a energia cinética da partícula em q