Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 2.5 - Ex. 39
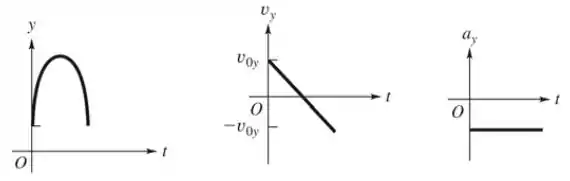
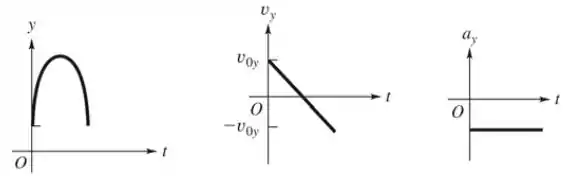
Uma bola de tênis em Marte, onde a aceleração devido à gravidade é de 0,379g e a resistência do ar é desprezível, é atingida diretamente para cima e retorna ao mesmo nível 8,5 s depois. (a) A que altura, acima do ponto de contato original, a bola subirá? (b) Em que velocidade ela estava se movendo logo depois de ser atingida? (c) Desenhe gráficos para a posição vertical da bola, a velocidade vertical e a aceleração vertical em função do tempo enquanto ela está no ar marciano.
Passo 1
E aiii galera!
Tudo bom com vocês?
Vamos fazer mais uma questãozinha?
Bom... o enunciado nos diz que uma bola de tênis em Marte, onde a aceleração devido à gravidade é de (em que )e a resistência do ar é desprezível, é atingida diretamente para cima e retorna ao mesmo nível depois.
Queremos calcular a que altura a bola subirá (acima do ponto de contato original) e a velocidade que ela estava se movendo logo depois de ser atingida.
Bom... Seja para cima.
na altura máxima e
As fórmulas de aceleração constante se aplicam:
Onde é a posição final, é a posição inicial, é a velocidade inicial, é o tempo, é a aceleração e é a velocidade final.
Passo 2
Letra a:
Considere o movimento da altura máxima de volta ao nível inicial. Para este movimento temos:
Assim, substituindo na equação da posição:
A bola foi acima de sua posição original.
Passo 3
Letra b:
Considere o movimento logo após ser atingido até a altura máxima. Para este movimento temos:
Então, aplicando na equação da velocidade:
Passo 4
Letra c:
Esboçando os gráficos da posição, da velocidade e da aceleração em função do tempo, temos, respectivamente:
