Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.8 - Ex. 47
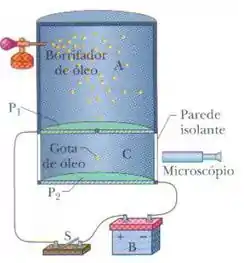
No experimento de Millikan, uma gota de óleo com um raio de 1,64 μm uma massa específica de permanece imóvel na câmara C (figura abaixo) quando um campo vertical de é aplicado. Determine a carga da gota em termos de e.
Passo 1
Fala aí! Como vai? 😎
Nesse problema foi mostrado o experimento de Milikan, onde uma gota de óleo permanece imóvel sabendo que a gota está sob um campo elétrico .
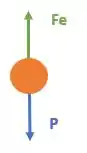
Pensa comigo: só temos duas forças atuando na gota: a força peso e a força eletrostática. O peso atua na gota para baixo. Então a força elétrica só pode atuar para onde? Para cima, correto? Correto, pois ele diz que ela permanece parada. Logo uma força tem que anular a outra.
Ele nos diz que o campo elétrico aplicado no tanque é vertical, mas não nos diz a direção. Olhando para o desenho, como o fundo do tanque está conectado no pólo negativo e a tampa do tanque está conectado no pólo positivo , e sabemos que as linhas de um campo elétrico apontam da carga positiva para a carga negativa, logo o campo elétrico está na vertical apontando pra baixo.
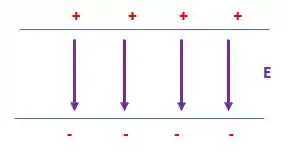
Se o campo está para baixo, mas a força aponta pra cima, a carga deve ser positiva ou negativa? Se liga na equação:
Se o campo elétrico está em um sentido e a força está no outro, os sinais dele são diferentes certo? Logo a carga deve ter um sinal negativo!
Passo 2
Nós já falamos que a força elétrica é dada por:
Onde é o valor do campo elétrico e é o valor da carga.
E a força peso é igual a:
Onde é a massa em kg e é a aceleração da gravidade.
Como falamos que as duas forças se cancelam, dado que a gota não se movimenta,podemos igualar o peso com a força elétrica:
Vamos isolar a carga:
Lembra que a gente tem a densidade de massa e o raio da gota . Então a gente tem a massa, certo?
Para isso é só lembrar o que é densidade:
Primeiro vamos calcular o volume, fazendo o volume de uma esfera.
A massa é a multiplicação da densidade pelo volume:
Logo:
Agora joga na equação da carga:
Passo 3
Agora é substituir os valores e correr pro abraço:
Lembra do sinal negativo, porque já discutimos que essa carga é negativa!
Quantas cargas elementares isso dá? Bom se a carga elementar vale Então:
E aí! O que achou? Responde Aí! 😁