Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 14.7 - Ex. 32bcd
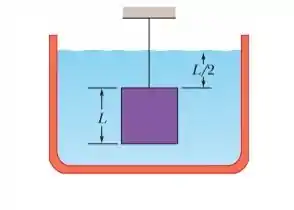
Na Fig 14-38, um cubo de aresta e de massa é suspenso por uma corda em um tanque aberto que contém um líquido de massa específica . Determine (a) o módulo da força total exercida sobre a face superior do cubo pelo líquido e pela atmosfera, supondo que a pressão atmosférica é , (b) o módulo da força total exercida sobre a face inferior do cubo e (c) a tensão da corda. (d) Calcule o módulo da força de empuxo a que o cubo está submetido usando o princípio de arquimedes. Que relação existe entre todas essas grandezas?
Passo 1
(b) Para calcular a força total atuante sobre a superfície inferior do cubo, vamos analisar a pressão total exercida nela pelo líquido e pela atmosfera. Para isso, vamos usar a expressão
Em que é a distância do nível do ponto analisado até a superfície da água. No caso:
Em (onde está localizada a superfície inferior do cubo), temos:
Substituindo os valores:
Passo 2
Lembrando que a relação entre força e pressão é , temos:
Substituindo os valores que já conhecemos :
Passo 3
(c) Podíamos usar o empuxo aqui. Onde a força de empuxo, é dada por:
Onde , pois é o volume do cubo.
Mas, como o problema pede exatamente isso na próxima letra, vamos fazer um pouquinho diferente:
Vimos que existem duas forças contrárias atuando sobre o cubo: uma na face superior, apontando para baixo, e outra na face inferior, apontando para cima, certo? E calculamos essas duas forças nas letras (a) e (b).
Dessa forma, podemos calcular a força resultante entre elas duas:
Substituindo os valores:
Repare que esse valor é beemmm próximo do empuxo. Não é coincidência ahaha pois esse é o processo para calcular o empuxo!! Então, na verdade e eram pra ser iguais! Essa pequena diferença é por conta das aproximações que fizemos ao longo das contas.
Além disso, o sinal negativo ali só indica que está na mesma direção da , ou seja, aponta para cima!
Mas essa força resultante é, sim, a força de empuxo!! Inclusive, vamos usar o valor para ficar mais exato, ok?
Passo 4
Agora, vamos olhar para o DCL do cubo:
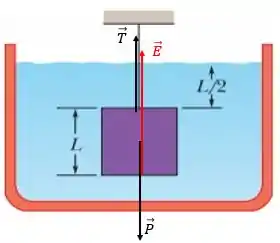
Onde é a tensão na corda, é a força peso do cubo e é o empuxo.
Pela segunda Lei de Newton, para o equilíbrio das forças, pois o corpo está suspenso:
Então, para calcular a tensão na corda:
Substituindo:
Show! Terminamos mais uma :D
Passo 5
(d) Opa, essa aqui, já até fizemos no passo 3. Ela pede para calcularmos o empuxo usando o Princípio de Arquimedes:
Onde , pois é o volume do cubo.
Beleza?? Acabou!