Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 21.4 - Ex. 8
Na Fig. 21-23, três esferas condutoras iguais possuem inicialmente as seguintes cargas: esfera ,; esfera, ; esfera , . As esferas e são mantidas fixas, a uma distância entre os centros que é muito maior que o raio das esferas. Dois experimentos são executados. No experimento , a esfera é colocada em fontato com a esfera , depois (separadamente) com a esfera e, finalmente, é removida. No experimento , que começa com os mesmos estados
iniciais, a ordem é invertida: a esfera é colocada em contato com a esfera , depois (separadamente) com a esfera e, finalmente, é removida. Qual é a razão entre a força eletrostática entre e no fim do experimento e a força eletrostática entre e no fim do
experimento?
Passo 1
Veja que essa questão é cheia de etapas, então, pra facilitar, bora analisar o problema por partes .
Na primeira etapa, a esfera neutra é colocada em contato com a , que estava com uma carga que . O que acontece quando elas encostam? A soma das cargas dessas duas esferas é distribuída igualmente entre as duas (por que elas são iguais, como o enunciado disse pra gente). Essa etapa a gente pode desenhar assim:
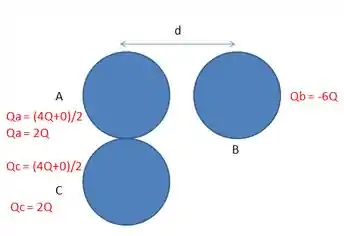
Passo 2
Depois, a esfera neutra encosta na esfera e o mesmo tipo de partilha acontece:
Agora, qual é a força eletrostática entre e depois de todo esse encosta-encosta do experimento ?
Passo 3
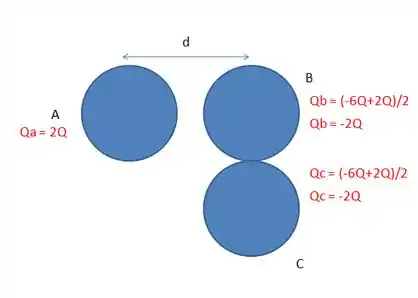
Agora, vamos pensar no experimento , em que a esfera , intrusa na relação entre e , encosta primeiro em e só depois em :
No primeiro contato, a soma total das cargas de e é dividida igualmente entre elas. Daí, cada uma fica com no final:
Passo 4
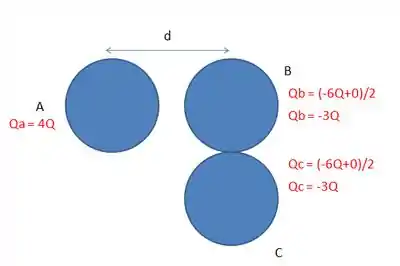
Agora, quando encostar em , acontece que a soma das cargas delas é dividida igualmente entre as duas (assim como anterioremente). Daí, a gente fica com essa situação:
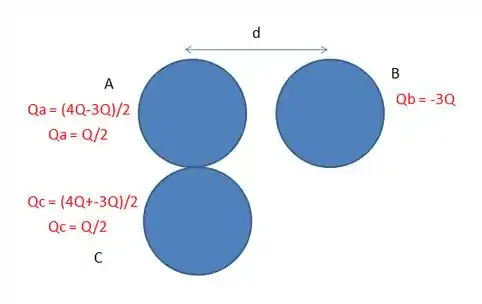
Depois desses contatos, a força elétrica entre e é igual a:
Dividindo as forças e , a gente encontra a resposta pedida: