Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 40
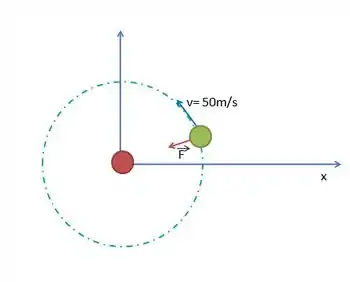
Uma partícula de carga é mantida fixa na origem de um sistema de coordenadas xy. No instante , uma partícula (, ) está situada no eixo , no ponto , e se move com uma velocidade de no sentido positivo do eixo y. Para que valor de a partícula executa um movimento circular uniforme? (Despreze o efeito da força gravitacional sobre a partícula.)
Passo 1
Nessa questão, ajuda bastante se tentarmos imaginar o que acontece através de um desenho. O que deve acontecer para que a partícula de carga mostrada na cor verde execute um movimento circular e uniforme?
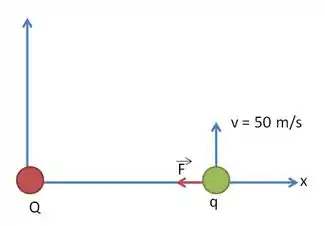
Para isso, você deve lembrar que em um movimento circular uniforme existe uma resultante de forças que é central e responsável pela mudança de direção e sentido do vetor velocidade. Essa resultante é a tal da resultante centrípeta.
Nesse caso, a nossa força centrípeta deve ser a força eletrostática entre as cargas. Essa força deve ser de caráter atrativo, pois, assim, é possível que a carga em verde faça um movimento circular em torno da carga vermelha.
Passo 2
Então, com base nisso, a gente tem a seguinte relação (sendo negativa, pois as cargas se atraem):
Isolando :
Sendo , , e valores dados no enunciado e a constante eletrostática igual a , aproximadamente.
Substituindo esses valores nessa expressão, a gente tem o resultado procurado:
Ou seja, se , a carga verde irá percorrer um movimento circular e uniforme, sendo a força centrípeta igual a força eletrostática de atração entre ela e a carga vermelha:
