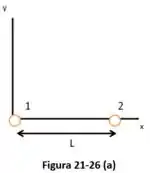
Na Fig. 21-27a, a partícula (de carga ) e a partícula (de carga ) são mantidas fixas no eixo, separadas por uma distância de . A força que as partículas e exercem sobre uma partícula (de carga ) colocada entre elas é . A Fig. 21-26b mostra o valor da componente dessa força em função da coordenada do ponto em que a partícula é colocada. A escala do eixo é definida por . Determine (a) o sinal da carga ; (b) o valor da razão .

A primeira coisa a se fazer para resolver a letra a) é analisar o gráfico da Figura Figura 21-26 (b). Como mostra esse gráfico, a força elétrica resultante possui valor máximo e positivo quando e estão muito próximas. Força positiva significa repulsão. Então, a gente já pode deduzir que é positiva, pois é positiva.

Beleza!, a gente sabe que as cargas e são positivas. O que deve acontecer para que esteja em equiíbrio entre e ? Veja as situações abaixo:

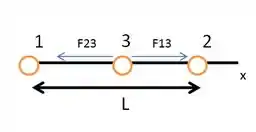
Suponha que as cargas e são ambas positivas. Então, nesse caso, as forças e que e exercem sobre são opostas em sentido, como mostra a figura abaixo. A mesma coisa acontece se elas duas forem negativas.

Agora, se e possuem sinais opostos (por exemplo, positiva e negativa), temos o caso abaixo:

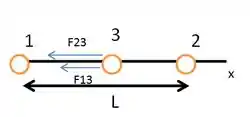
Veja que, assim, se e tiverem sinais opostos, então não é possível que esteja em equilíbirio.

Tranquilo até aqui? 😉

Além disso, o gráfico da Figura Figura 21-26 (b) mostra pra gente que a força é nula quando a partícula está na abscissa . Usando esse fato na equação da força elétrica total, temos:

Dividindo os dois lados por ...

Isolando ...

E aí! entendeu tudo? Responde Aí! 😁