Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 29.3 - Ex. 38
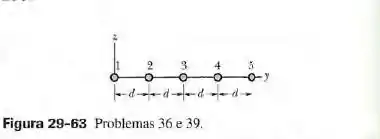
Na figura 29-63, cinco fios paralelos longos no plano estão separados por uma distância , têm de comprimento e conduzem correntes iguais de para fora do papel. Em termos dos vetores unitários, determine a força (a) sobre o fio 1. (b) sobre o fio 2; (c) sobre o fio 3; (d) sobre o fio 4; (e) sobre o fio 5.
Passo 1
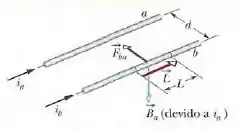
A força entre duas correntes paralelas na presença do campo magnético externo é dada por:
em que é o vetor comprimento do fio. Podemos ver na figura acima, os vetores e são mutuamente perpendiculares e, portanto, de acordo com a equação para fios retilíneos longos, podemos escrever:
Podemos usar essa queção para calcular o módulo da força entre os fios. Para a força magnética a que está submentido o fio 1:
Passo 2
Agora, vamos lá calcular a força magnética no fio 2!
A força exercida pelo fio 1 sobre o fio 2 cancela a força exercida pelo fio 3 sobre o fio 1 😉
Passo 3
Vamos analisar a situação do fio 3. Como nossos fios estão separados igualmente, o fio 3 está exatamente no meio da disposição deles no espaço. Como em todos os fios temos a mesma intensidade de corrente e mesmo sentido, temos que os fios que está a direita do fio 3 geram um campo resultando nele para baixo; os fios situados a esquerda do fio 3 geram um campo resultado nele para cima. Esses campos são iguais em módulo e geram um campo resultante no fio 3 igual a zero! Logo,
Passo 4
Para o fio 4 teremos a mesma situação que foi para o fio 2, diferenciando apenas o sentido da força. Como no fio 2 tivemos orientação positiva para o vetor , para o fio 4 teremos:
Passo 5
Para o fio 5 teremos a mesma situação que foi para o fio 1, diferenciando apenas o sentido da força. Como no fio 1 tivemos orientação positiva para o vetor , para o fio 5 teremos:
Resposta
- ;
- ;
- ;