Na Fig. 23-41 , um pequeno furo circular de raio foi aberto no meio de uma placa fina, infinita, não condutora, com uma densidade superficial de cargas

. O eixo , cuja origem está no centro do furo, é perpendicular à placa. Determine, em termos dos vetores unitários, o campo elétrico no ponto , situado em . (Sugestão: use a Eq. 22-26 e o princípio de superposição.)

Considere que o campo resultante do sistema Plano infinito perfurado é equivalente à superposição dos campos causados pelos sistemas Plano infinito e Disco de raio R com densidade de carga . Assim:

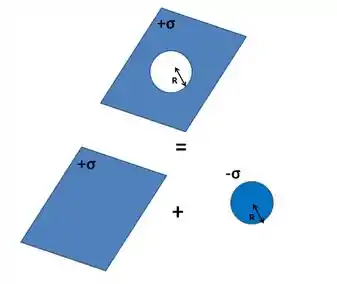
Fazemos isso simplesmente porque um orifício significa uma ausência de carga. E essa ausência equivale à “soma”, ou superposição, de cargas de módulos iguais e sinais contrários.

Beleza!

Então, agora, vamos achar o campo elétrico devido a cada um desses sistemas que estamos superpondo.

Primeiro, vamos trabalhar com o plano infinito de densidade superficial de carga . Lembra como podemos encontrar o campo resultante da distribuição de cargas num plano assim? Ele é dado pela fórmula:

Agora, preste atenção no disco idealizado, com densidade superficial de carga igual a . Vamos calcular o campo elétrico resultante desse disco. Para isso, vamos novamente dividir esse disco em pequenos anéis de raio r e calcular primeiro o campo resultante de cada um desses anéis. Fazendo isso a gente tem o seguinte:

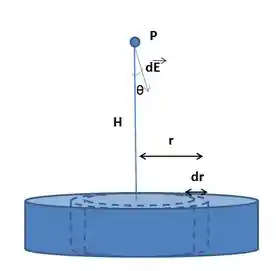
Disco de densidade superficial de cargas Um dos anéis que formam o disco quando somados.

Olhando para o anel da figura da direita, vamos somar os campos produzidos por cada uma das unidades de carga , que equivalem às cargas de pequenos setores circulares de abertura infinitesimal . Cada campo desse setor é equivelente ao campo produzido por uma carga pontual:

Mas, nesse caso, a gente só considera a componente vertical desse campo, pois na horizontal as componentes dos campos das outras unidades de carga se cancelam.

Assim, a gente tem que:

Para acharmos a resultante vertical do campo devido a um anel, devemos integrar em , de zero a . Assim:

Agora, para acharmos a soma dos campos devidos aos anéis, que resulta no campo do disco, devemos integrar a expressão acima em :

Resolvendo a integral acima , temos:

Sendo:

Então:

Beleza! Agora, é só a gente usar a superposição desses sistemas:

Então: