Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.7 - Ex. 26
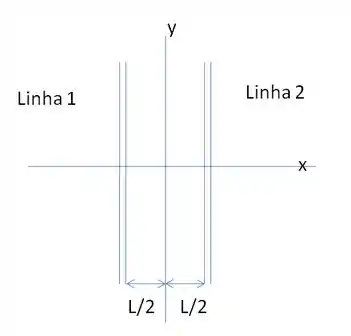
Na Fig. 23-39, pequenas partes de duas linhas paralelas de cargas muito compridas são mostradas, fixas no lugar, separadas por uma distância . A densidade uniforme de cargas das linhas é para a linha e para a linha . Em que ponto do eixo o campo elétrico é zero?
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui oque queremos é encontrar em qual ponto a resultante dos campos elétricos gerados pelas linhas paralelas é nulo.
Usaremos aqui o conceito da lei de gauss pra encontrar o campo nas linhas paralelas de cargas isso para cada uma das linhas.
Precisaremos fazer o somatório dos campos dessas linhas em função de uma posição que queremos encontrar, após isso combinaremos esses campos e igualaremos a zero já que o enunciado quer tal que o campo no ponto seja nulo.
Passo 2
- Usando a Lei de Gauss, a gente pode encontrar o campo elétrico devido a uma linha carregada, a uma distância dela. Fazendo assim, temos:
Por serem constantes o campo e a área saem da integral:
Onde a área será a área lateral do cilindro da superfície Gaussiana.
Como o raio desse cilindro está no eixo , vou escrever assim:
Aqui usaremos o conceito de densidade linear de cargas fazendo:
E substituindo na equação do campo, teremos:
E esse é o campo gerado por uma linha de cargas, beleza?
Olha aí, o nossos apareceu em algum lugar, vamos acha-lo jajá.
Passo 3
Beleza! A gente achou o campo elétrico causado por uma linha infinita carregada qualquer.
Bora usar esse resultado nessa questão!
Considera que é a distância de um ponto à linha da esquerda, com de densidade linear de carga.
Nesse caso, é a distância desse ponto até a outra linha, que possui de densidade linear de carga.
Daí, o campo elétrico total nesse ponto é dado pela soma dos campos devidos a cada linha :
Substituindo os dados temos:
Pra resolver vamos cortar todo mundo que é parecido, pega a tesoura aí, e a equação ficará com essa cara:
Nada mal mas dá pra melhorar:
Multiplicando cruzado teremos:
Isolando :