Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 40
Considere a esfera sólida condutora e a casca esférica condutora concêntrica na Figura 22-31. A casca esférica tem carga . A esfera sólida tem carga . (a) Quanta carga está na superfície externa e quanta carga está na superfície interna da casca esférica? (b) Considere, agora, que um fio metálico seja conectado entre a esfera sólida e a casca. Depois de o equilíbrio eletrostática ser restabelecido, quanta carga está na esfera sólida e em cada superfície da casca esférica? O campo elétrico na superfície da esfera sólida varia quando o fio é conectado? Se a resposta for positiva, de que maneira? (c) Considere as mesmas condições da parte (a), com na esfera sólida e na casca esférica. Aterramos, então, a esfera sólida através de um fio metálico e, em seguida, desconectamos o fio. Neste caso, qual é a carga total na esfera sólida e em cada superfície da casca esférica?
Passo 1
Falaa galerinha. Mais um exercício complicadinho, né?! Mas vamos lá :D
Nesse exercício devemos lembrar o conceito de indução. Note que e a esfera dentro da casca esférica irá induzir cargas da casca. Além disso, devemos lembrar que quando conectados um fio ideal entre condutores, eles se comportam como se fosse apenas um condutor! Vamos aplicar essas ideais?
Passo 2
- Veja a figura esquemática
- Quando o fio é conectado, as esferas se comportam como se fossem apenas um condutor... e como sabemos, toda a carga livre vai para a superfície mais externa do condutor. Assim, veja a figura abaixo:
- Agora, aterramos a esfera externa. Isso faz com que toda a carga na superfície externa dela vá para a terra!! Assim, temos a seguinte configuração de cargas.
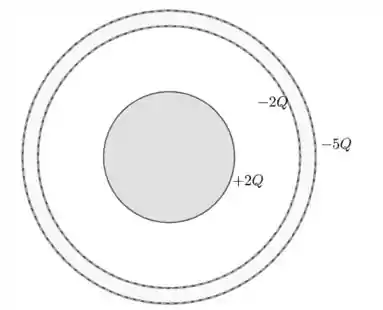
Repare que a esfera interna induz uma carga na superfície interna da casca esférica. Como a carga simplesmente não pode sumir, a parte externa deve ficar com carga (note que a carga total da casca ainda continua ).
Passo 3
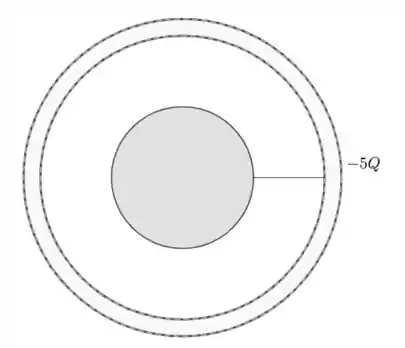
Dessa forma, o campo da esfera interna varia... ele vira zero :D
Passo 4
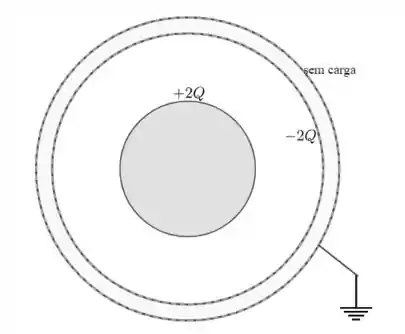
Portanto, a configuração de cargas fica como mostrado na figura. A carga total na esfera sólida continua e na casca .
Resposta
- Veja o esquema
- O campo vai para zero.
- Veja o esquema