Uma fina casca esférica não condutora de raio tem uma densidade superficial uniforme de carga de . (a) Qual é a carga total na casca? Determine o campo elétrico nas seguintes distâncias ao centro da esfera: (b) 2,00 cm, (c) 5,90 cm, (d) 6,10 cm e (e) 10,0 cm.
Passo 1
Fala galerinha, tudo blz? Bem, então temos um caso de simetria esférica. Os casos de simetria esférica devemos usar a lei de Gauss usando uma esfera como sendo
Passo 2
- Como a densidade é constante, a carga total será simplesmente a densidade vezes a área da esfera (que é , sendo o raio da esfera). Logo,
Passo 3
Vamos usar a simetria esférica para calcular o campo dentro da esfera para
- Pontos interno, ou seja,
- Para pontos externos, :
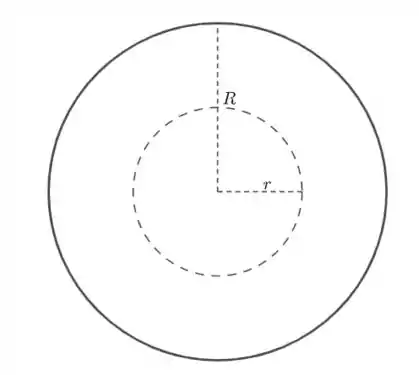
Como
Como , segue que . Assim, para pontos internos da casca esférica, o campo elétrico é sempre zero.
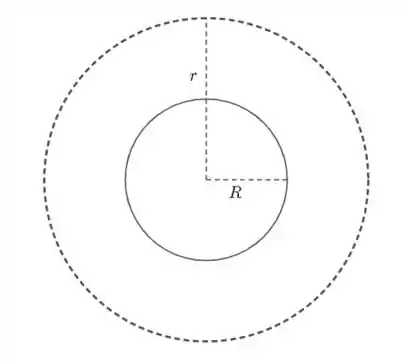
Nesse caso, . Logo,
Tendo essas duas fórmulas em mãos, podemos calcular o campo elétrico em cada ponto: