Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.9 - Ex. 48
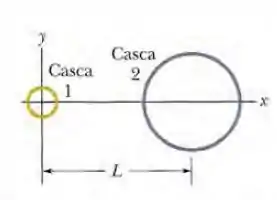
A Fig. 23-51 mostra duas cascas esféricas não condutoras mantidas fixas no lugar sobre o eixo . A casca possui uma densidade uniforme de cargas superficiais na superfície externa e um raio de , enquanto a casca possui uma densidade uniforme de cargas superficiais na superfície externa e um raio de ; a distância entre os centros é . Determine o(s) ponto(s) sobre o eixo x (além do infinito) onde o campo elétrico é zero.
Passo 1
Fala aí! Tudo certinho? 😁
Nesse problema temos duas cascas esféricas com densidades e . Enquando a esfera menor tem raio , a esfera maior tem raio . Se a distancia entre os centros das esferas é , qual é o ponto onde o campo elétrico é ?
O que deve acontecer para que o campo seja nulo em algum ponto?
- É necessário que os campos devidos a cada casca estejam na mesma direção e em sentidos contrários;
- É preciso, também, que os módulos desses campos sejam iguais.
Igualando, então, os campos devidos a cada casca, temos o seguinte:
Sacou? Bora começar! 🤔
Passo 2
Da expressão anterior, temos que:
Como a área de uma esfera de raio é dada por , isolando na equação acima, temos:
Como , então:
E aí! Entendeu tudo? Responde Aí! 😎
