Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 8º - Capítulo 23.9 - Ex. 52

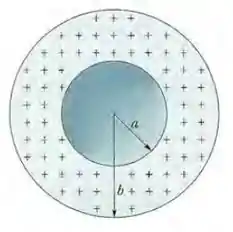
A Fig. 23-53 mostra uma casca esférica com uma densidade volumétrica de cargas uniforme ρ   =   1,84   n C / m 3 , raio interno a   =   10,0   c m e raio externo b   =   2,00 a . Determine o módulo do campo elétrico (a) em r   =   0 ; (b) em r   = a 2,00 ; (c) em r   =   a ; (d) em r   = 1,50 a ; (e) em r   =   b ; (f) em r   =   3,00 b .

Passo 1

Shoooow galerinha, vamos continuar?

Belezaaa !!

Antes de qualquer coisa vamos lembrar como se calcula o campo elétrico?

E = 1 4 π ϵ 0 q i n t r 2

Antes de aprofundar aqui e calcularmos a carga interna da esfera nós vamos citar uma informação bem importante, que vai resolver a letra (a) rapidinho !

O invólucro esférico é um condutor, assim as cargas induzidas são desenvolvidas na superfície da casca. E o que isso significa?

Que não vai haver carga disponível no centro do invólucro, nem dentro do invólucro !!

Ou seja, quando r ≤ a teremos q i n t = 0   C e, consequentemente, o campo elétrico também será zero !!

Em quais opções nós temos r ≤ a ?? Nas letras (a), (b) e (c), certo?

Então nestes três casos já sabemos que o campo elétrico vale zero !!

Passo 2

Para dar continuidade nós vamos lembrar como calculamos a carga interna em uma casca esférica, que está representada aqui pelo azul claro !!

A fórmula que nós usamos nesses casos é:

q i n t = 4 3 π ρ ( r 3 - a 3 )

Substituindo no campo elétrico:

E = 1 4 π ϵ 0 4 3 π ρ ( r 3 - a 3 ) r 2

E = ρ 3 ϵ 0 r - a 3 r 2

Quando r = 1,5 a :

E = ρ 3 ϵ 0 1,5 a - a 3 1,5 a 2 = 1,0556 . ρ a 3 ϵ 0

Sabendo que:

ρ   =   1,84 × 10 - 9 C m 3

a   =   0,10   m

ϵ 0 =   8.85 × 10 - 12   C 2 N m 2

Substituindo:

E = 1,0556 . 1,84 × 10 - 9 C m 3 0,10   m 3 8.85 × 10 - 12   C 2 N m 2

E = 7,3 N C

Passo 3

Agora, na letra (e)m quando r = b = 2 a :

E = ρ 3 ϵ 0 2 a - a 3 2 a 2 = 1,75 . ρ a 3 ϵ 0

Substituindo novamente os dados:

E = 1,75 . 1,84 × 10 - 9 C m 3 0,10   m 3 8.85 × 10 - 12   C 2 N m 2

E = 12,1 N C

Na letra (f), r   =   3,00 b = 6 a , ou seja, bem maior que o raio externo que é 2 a ! Neste caso o campo elétrico é calculado de forma diferente, preparados?

E = 1 4 π ϵ 0 q r 2

Presta bastante atenção nesse ponto, quando a gente usa uma distância maior que a da superfície onde temos cargas envolvidas o raio do numerador vai ser diferente do raio do denominador, pois o máximo valor de raio onde contemos cargas é o valor b .

E = 1 4 π ϵ 0 4 3 π ρ ( r 1 3 - a 3 ) r 2

Então sabendo que o máximo valor de r 1 = b temos a seguinte situação:

E = ρ 3 ϵ 0   b 3 - a 3 r 2

Substituindo o raio e b:

E = ρ 3 ϵ 0   2 a 3 - a 3 ( 6 a ) 2 = ρ 3 ϵ 0   8 a 3 - a 3 36 a 2

E = ρ a 3 ϵ 0 7 36

Susbtituindo:

E = 1,84 × 10 - 9 C m 3 0,10   m 3 8.85 × 10 - 12   C 2 N m 2 7 36

E = 1,35 N C

E chegamos ao fim de mais uma galeraa !!

Resposta

  1. E = 0 N C
  2. E = 0 N C
  3. E = 0 N C
  4. E = 7,3 N C
  5. E = 12,1 N C
  6. E = 1,35 N C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma carga pontual q=1,0 × 10 - 7C é colocada no centro de uma cavidade esférica com 3,0c m de raio aberta em um bloco de metal. Use a lei de Gauss para determinar o campo elétrico (a 1,5c m de distânc
Uma placa infinita de espessura insignificante, situada no plano xy, possui uma densidade superficial de cargas uniforme ρ = 8,0 n C / m 2 . Determine o fluxo elétrico através de uma esfera gaussiana
Uma placa infinita que ocupa o espaço entre os planos x= -5,0c m e x =+ 5,0c m tem uma densidade volumétrica de cargas uniforme p=1,2n C / m 3 . Determine o módulo do campo elétrico (a) no planox=4,0c
O mistério do chocolate em pó. Explosões provocadas por descargas elétricas (centelhas) constituem um sério perigo nas indústrias que lidam com pós muito finos. Uma dessas explosões aconteceu em uma f
Na Fig. 23-29, um próton se encontra a uma distância vertical d/2 do centro de um quadrado de aresta d. Qual é o módulo do fluxo elétrico através do quadrado? (Sugestão: pense no quadrado como uma das