Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 22.5 - Ex. 19
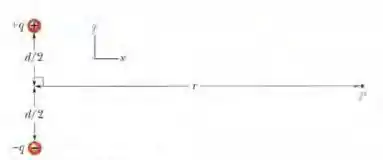
A Fig. abaixo mostra um dipolo elétrico. Determine (a) o módulo e (b) a orientação (em relação ao semieixo x positivo) do campo elétrico produzido pelo dipolo em um ponto P
Situado a uma distância
Passo 1
Fala aí! Tudo certinho? 😁
Nesse problema foi dado um dipolo elétrico e nosso objetivo é obter o campo elétrico (modulo e orientação) em um ponto a uma distância em que e é a distância entre os polos do dipolo.
Tem ideia de como fazer isso? 😬
Primeiramente, nós temos que saber a orientação dos vetores campo elétrico devido as duas cargas. Como as cargas são iguais, e lembrando que carga positiva tem campo divergente (afastamento) e carga negativa tem campo convergente (aproximação), podemos fazer o desenho do campo resultante:
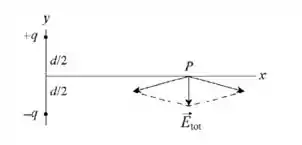
Note que a componente dos campos no eixo x se anulam, devido a cargas serem de iguais módulos, sobra somente a componente no eixo x. O campo devido a cada carga é igual em módulo (cargas iguais em módulo e o ponto P está a mesma distância das duas cargas). Chamaremos de o ângulo entre o campo devido a carga negativa e o eixo x.
Passo 2
Item (a)
Para calcular o , devemos multiplicar o campo devido as cargas por , isto é, pegar apenas a componente y. Lembrando-se da trigonometria, . Assim,
Para , , assim, a expressão se reduz a:
Tranquilo até aqui? 😉
Passo 3
Item (b)
Como vimos na figura, o campo elétrico aponta para a parte negativa do eixo y, ou seja, faz um ângulo de com o semieixo x positivo.
E aí! O que achou? Responde Aí! 😉
