Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.6 - Ex. 20
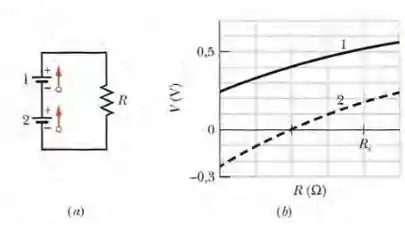
Na Fig. 27-32a, as duas fontes têm uma força eletromotriz e a resistência externa R é um resistor variável. A Fig. 27-32b mostra as diferenças de potencial V entre os terminais das duas fontes em função de R: a curva 1 corresponde à fonte l e a curva 2 corresponde à fonte 2. A escala horizontal é definida por . Determine (a) a resistência interna da fonte l; (b) a resistência interna da fonte 2.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui queremos encontrara a resistência interna das fontes dadas, com auxílio do gráfico que mostra a ddp da fontes em relação a resistência .
Passo 2
(a) Vamos chamar de e as fem das fontes. De acordo com a regra das malhas,
A diferença de potencial entre os terminais da fonte 1 é e a diferença de potencial entre os terminais da fonte 2 é , na qual e são as resistências internas das fontes 1 e 2, respectivamente. Assim,
De acordo com o enunciado, . De acordo com o gráfico da Fig. 27-32b, e para R = 0,10 Ω. Substituindo esses valores nas equações anteriores, obtemos um sistema de duas equações com duas incógnitas, e .
Passo 3
(b) Substituindo em:
Resposta
(a)
(b)