Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 15

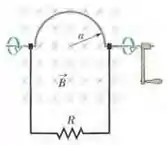
Na Fig. 30-48, uma semicircunferência de fio de raio a = 2,00   c m gira com uma velocidade angular constante de 40 revoluções por segundo na presença de um campo magnético uniforme 20   m T . Determine (a) a frequência e (b) a amplitude da força eletromotriz induzida no circuito.

Passo 1

E aí, pessoal! 😊

Como ilustrado na figura, a questão fornece uma semicircunferência que gira com uma velocidade angular constante ω = 40 r e v s = 40 ⋅ 2 π r a d s .

Devido à essa rotação, a área limitada pelo circuito varia, de modo que o fluxo magnético também vai variar, induzindo uma força eletromotriz.

É isso que devemos calcular!

Parece complicado? 👀

Passo 2

No item (a), queremos a frequência de rotação:

ω = 2 π f → f = ω 2 π

f = 40 ⋅ 2 π 2 π   H z

f = 40   H z

Note que nem precisaríamos fazer conta pois a questão já fornecer a velocidade angular em unidade de frequência...

Tranquilo até aqui? 😉

Passo 3

Para calcular a fem induzida, precisamos primeiro calcular o fluxo como função do tempo. Como o campo magnético B = 20   m T é constante, devemos no preocupar mais com a área!

A área do circuito pode ser quebrada em duas partes: um retângulo de área fixa A 0 e um semicírculo de área π a 2 / 2 .

A área A 0 é sempre normal ao campo magnético, de modo que sua contribuição para o fluxo será constante e igual a B A 0 . Já para o semicírculo, conforme ele rotacional, o ângulo θ   entre o campo magnético e a normal ao plano varia como θ = ω t = 2 π f t . Assim, o fluxo será

Φ B = ∫ B → ⋅ d A → = B A 0 + B ⋅ π a 2 2 ⋅ cos ⁡ θ

Φ B = B A 0 + B π a 2 2 cos ⁡ ( 2 π f t )

Bacana, não é? 😁

Passo 4

Pela lei de Faraday, temos que

ε = - d Φ B d t

Assim, como B A 0 é constante:

ε = - B π a 2 2 ⋅ 2 π f ⋅ - s e n   2 π f t

Portanto,

ε = π 2 B a 2 f   s e n   2 π f t

A amplitude é apenas a parte que multiplica o seno:

ε m = π 2 B a 2 f = 3,14 2 ⋅ 0,020   T ⋅ 0,020   m 2 ⋅ 40   s - 1

Assim,

ε m = 3,2 ⋅ 10 - 3   V

E aí! o que achou? Responde Aí! 😊

Resposta

f = 40   H z

ε m = 3,2 ⋅ 10 - 3   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espira retangular, com uma área de 0,15m 2 , está girando na presença de um campo magnético uniforme de módulo B = 0,20T . Quando o ângulo entre o campo e a normal ao plano da espira é π / 2 e est
Na Fig. 30-54, uma espira retangular de comprimento a = 2,2c m , largura b = 0,80c m e resistência R = 0,40m Ω é colocada nas vizinhanças de um fio infinitamente longo percorrido por uma corrente i =
Na Fig. 30-48, uma espira quadrada com 2,0c m de lado é submetida a um campo magnético, dirigido para fora do papel, cujo módulo é dado por B = 4,0 t 2 y , onde B está em teslas, t em segundos e y em
No sistema da Fig. 30-47, a = 12,0c m e b = 16,0c m . A corrente no fio retilíneo longo é dada por i = 4,50 t 2 - 10,0 t , onde i está em ampères e t em segundos. (a) Determine a força eletromotriz na
A Fig. 30-45 mostra duas espiras paralelas com um eixo comum. A espira menor (de raio r ) está acima da espira maior (de raio R ) a uma distância x ≫ R . Em consequência, o campo magnético produzido p