Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.4 - Ex. 19
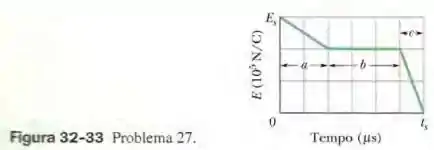
Na Fig. 32-33, um campo elétrico uniforme é reduzido a zero. A escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . Calcule o módulo da corrente de deslocamento através de uma área de perpendicular ao campo durante os intervalos de tempo , e mostrados no gráfico.
Passo 1
O problema fornece o gráfico de um campo elétrico que varia no tempo e quer que calculemos a corrente de deslocamento em diferentes intervalos de tempo. Para isso, devemos lembrar que ela é dada por
Por outro lado, como e a área é constante
Portanto,
Como a variação de com o tempo é linear:
Além disso, como faremos as contas em módulo:
Passo 2
No intervalo , temos que
Assim,
Assim, usando :
Para o trecho , temos que , de modo que
Passo 3
Já no item (c), temos que e de modo que
Portanto,