Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.7 - Ex. 36
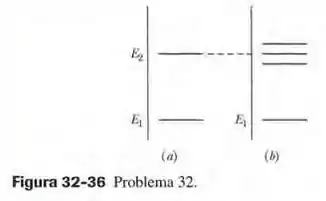
A Fig. 32-36a mostra dois valores permitidos de energia (níveis de energia) de um átomo. Quando o átomo é submetido a um campo magnético de , os níveis de energia mudam para os que aparecem na Fig. 32-36b por causa da energia associada ao produto escalar . (Estamos ignorando o efeito de .) O nível não é alterado, mas o nível se desdobra em três níveis muito próximos. Determine o valor de associado (a) ao nível de energia ; (b) ao nível de energia . (c) Qual é o valor em joules do espaçamento entre os níveis desdobrados?
Passo 1
Esse problema retrata a quebra de degenerescência do átomo de hidrogênio na presença de um campo externo, que é tratado em detalhe em cursos de mecânica quântica. Mas relaxa, não vamos precisar recorrer a ela para resolver esse problema!
Vamos lembrar que a energia potencial associada à interação de momento magnético com um campo externo é dada por
Neste caso, estamos considerando apenas o momento magnético orbital, de modo que
Assim, como a componente do momento angular orbital é quantizada, as equações 32-31 e 32-32 estabeleceram que
onde é o famoso magnéton de Bohr. Assim, os níveis de energia, na presença de campos magnéticos, serão dados por
Passo 2
Note que para não há desdobramento em outros níveis de energia, de modo que para esse estado, temos que , de modo que
Já para os estados , temos a quebra em três níveis de energia distintos, sendo um deles com a mesma energia de antes (). Assim, neste caso, temos três valores possíveis:
Passo 3
Por fim, como sabemos que, para os estados , , as diferenças entres os níveis será
Lembrando que e usando , obtemos