Na Fig. 35-44, uma fonte luminosa com um comprimento de onda de ilumina perpendicularmente duas placas de vidro de de comprimento que se tocam na extremidade esquerda e estão separadas por uma distância na extremidade direita. O ar entre as placas é como um filme fino. Quantas franjas claras são vistas por um observador que olha para baixo através da placa superior?

O problema fala sobre um filme fino de ar em formato de cunha, como mostra a figura:

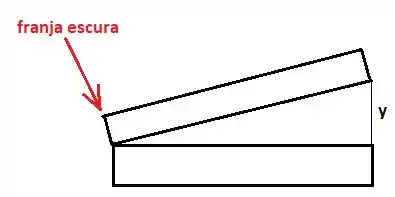
Como o filme de ar está entre as laminas, a primeira reflexão ocorre na interface entre o vidro e o ar, de modo que não inversão de fase, enquanto a segunda ocorre do ar pro vidro, ocorrendo inversão. Como em um reflexão a fase inverte e na outra não, devemos adicionar na defasagem:

A diferença de caminho será :

Como , a expressão fica:

Para que haja interferência:

Se for par, ela será construtiva, se for ímpar ela será destrutiva. Assim,

Sabemos que na extremidade esquerda . Assim, temos que a primeira franja escura corresponde a .