Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 35.Problemas - Ex. 46
Uma película uniforme fina de um material com índice de refração reveste uma placa de vidro de índice de refração . Essa película tem a espessura adequada para cancelar uma luz de comprimento de onda que incide perpendicularmente a partir do ar sobre a superfície da película, mas é um pouco maior do que a espessura mínima necessaria para efetuar esse cancelamento. Com o passar do tempo, a película de desgasta a uma taxa constante de por ano. Qual é o número mínimo de anos para que a luz refletida com esse comprimento de onda passe a ser reforçada em vez de cancelada?
Passo 1
Vamos pensar no seguinte: se a luz estava sofrendo interferência destrutiva, o que a gente pode afirmar sobre a diferença de caminho?
Bom, com certeza ela seguia essa fórmula aqui:
Se você quer atingir interferência construtiva, então tem que passar a obedecer essa fórmula aqui:
Então a variação da diferença de caminho é:
Ou seja, a diferença de caminho tem que diminuir em meio comprimento de onda!
Mas já que estamos lidando com um índice de refração diferente no material, temos que ajustar o comprimento de onda pelo índice , então:
Passo 2
Agora vamos ver como essa diferença de caminho se relaciona com a espessura da camada:
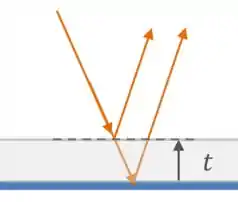
Então, considerando a “ida e a volta” da luz na camada:
Ou seja:
Substituindo com a equação do passo de cima:
Passo 3
Se a película se desgasta por por ano, então para desgastar , o tempo necessário é:
Ou seja, a luz vai deixar de ser “cancelada” depois de aproximadamente anos.
Resposta
A luz passará a ser reforçada após cerca de anos.