Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.Problemas Adicionais - Ex. 89
Na Fig. 35-52, um transmissor de micro-ondas situado a uma altura a acima do nível da água de um lago transmite micro-ondas de comprimento de onda em direção a um receptor na margem oposta, situado a uma altura x acima do nível da água. As micro-ondas que se propagam diretamente através do ar. Supondo que a largura D do lago é muito maior que a e x que , para que valores de x o sinal que chega ao receptor tem a maior intensidade possível? (sugestão: verifique se a reflexão resulta em uma mudança de fase.)
Passo 1
Nós podemos simplificar o problema para a seguinte figura:
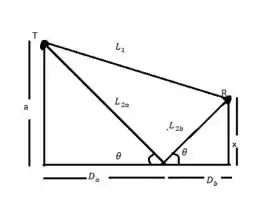
A onda que irá chegar ao receptor percorre uma distância e a onda refletida percorre uma distância . O índice de refração da água é maior que o do ar, a onda que é refletida sofre uma variação na sua fase de meio comprimento de onda.
Então para que tenhamos uma interferência construtiva na onde o receptor tá, a diferença de percurso deve ser um múltiplo ímpar de meio comprimento de onda.
Olhando na figura temos um triângulo retângulo mais à esquerda, aplicando a , e o triângulo mais à direita teremos .
Passo 2
Como
Manipulando a expressão assim nós teremos:
Logo
Passo 3
Geralmente D é muito maior que x e d logo podemos expandir em Taylor:
indo pela esquerda.
indo pela direita.]
Logo a diferença de percurso para que haja interferência construtiva temos que
Assim os valores em que x é construtivo será:
Resposta