Enunciado
Física - Halliday - Vol 4- Ed: 9º - Capítulo 35.8 - Ex. 83
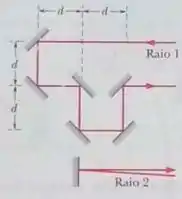
Dois raios luminosos, inicialmente em fase e com um comprimento de onda de , percorrem diferentes trajetórias sofrendo reflexões em espelhos planos, como mostra a Fig. 35-48. (As reflexões não produzem mudanças de fase). (a) Qual é o menor valor de para o qual os raios têm fases opostas ao deixarem a região? (Ignore a ligeira inclinação da trajetória do raio 2). (b) Repita o problema supondo que o sistema está imerso em uma solução de proteínas com um índice de refração de .
Passo 1
Esse é um problema clássico sobre interferência devido à diferença de caminho! Note que o raio 1 percorre uma distância extra com relação ao raio 2 de . Portanto,
Como queremos que as fases sejam opostas (interferência destrutiva), a diferença de caminho deve ser um múltiplo semi-inteiro do comprimento de onda:
O menor valor de ocorre para :
Portanto,
Passo 2
Se o sistema for mergulhado numa solução de proteínas com , o comprimento de onda é alterado para
Assim,