Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.Problemas Adicionais - Ex. 92
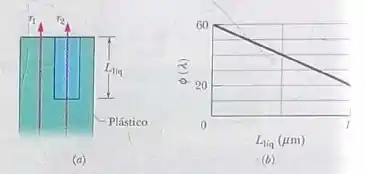
A Fig 35-55ª mostra dois raios luminosos, com um comprimento de onda no ar de 400nm, que estão inicialmente em fase enquanto se propagam para cima de um bloco de plástico. O raio atravessa o plástico e chega ao ar. Antes de chegar ao ar, o raio passa por um líquido contido em uma cavidade do plástico. A altura do líquido é inicialmente começa a evaporar. Seja a diferença de fase entre os raios ao chegarem ao ar. A Fig.35-55b mostra o valor de do líquido, com em comprimentos de onda e a escala do horizontal definida por . Determine (a) o índice de refração do plástico (b) o índice de refração do líquido.
Passo 1
- Vamos chamar de L a profundidade da cavidade, e vamos chamar o índice de refração do plástico e o índice do líquido. Analisando o gráfico nós temos que quando é zero a diferença de fase é 60 comprimentos de onda, está diferença de fase é igual a diferença entre o número de comprimentos de onda na distância L no plástico (para o raio e também para o ar( para o raio
- Utilizando o fato do item a nós teremos:
Assim nós teremos:
Passo 2
Podemos pegar um ponto da reta 35-55b por exemplo .
Assim
Resposta
a)
b)
Exercícios de Livros Relacionados
Na Fig.35-50a, as ondas associadas aos raios 1 e 2 estão inicialmente em fase e têm, o mesmo comprimento de onda λ no ar. O raio 2 atravessa um material de comprimento L e índice de refração n. Os rai
Na Fig. 35-50a, as ondas associadas aos raios 1 e 2 estão inicialmente em fase e têm o mesmo comprimento L e índice de refração n. Os raios são refletidos por espelhos para um ponto em comum P, situad