Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 12

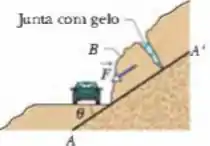
A Fig. 6-22 mostra que a seção transversal de uma estrada na encosta de uma montanha. A reta A A ' representa um plano de estratificação ao longo do qual pode ocorrer um deslizamento. O bloco B , situado acima da estrada, está separado do resto da montanha por uma grande fenda (chamada junta), de modo que somente o atrito entre o bloco e o plano de estratificação evita o deslizamento. A massa do bloco é 1,8 × 10 7   k g , o ângulo de mergulho θ do plano de estratificação é 24 ° e o coeficiente de atrito estático entre o bloco e o plano é 0,63 . (a) Mostre que o bloco não desliza. (b) A água penetra na junta e se expande após congelar, exercendo sobre o bloco uma força F → paralela a A A ' . Qual é valor mínimo do módulo F da força para o qual ocorre um deslizamento?

Passo 1

Esta é uma questão que a interpretação e a visualização dificulta um pouco. Por isso, vamos começar fazendo um ilustração simplificada do nosso problema:

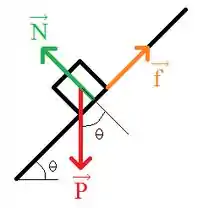
Logo, percebemos que este é um exercício clássico de plano inclinado, show? Por isso, vamos iniciar escrevendo a segunda lei de Newton para cada eixo:

f - P sin ⁡ θ = m a x       e q . 1

N - P cos ⁡ θ = m a y       e q . 2

Além disso, precisamos ter em mente que podemos determinar o módulo da força de atrito estático máximo ( f s m á x ) através da seguinte relação:

f s m á x = μ s N       e q . 3

Passo 2

Vamos começar definindo a normal usando a e q . 2 :

N - P cos ⁡ θ = m a y

Como não há movimento no eixo y :

N - P cos ⁡ θ = 0

Isolando N e substituindo os valores conhecidos:

N = 1,8 × 10 7 × 9,8 × cos ⁡ 24 ° = 16 × 10 7   N

Passo 3

Com o valor da normal em mãos, podemos usar a e q . 3 substituindo os valores conhecidos para determinar f s m á x :

f s m á x = 0,6 3 × 16 × 10 7 = 10 , 08 × 10 7   N

Passo 4

Agora, supondo que no eixo x não haja movimento, então a e q . 1 se reduz a:

f - P sin ⁡ θ = 0

Isolando f e substituindo os valores conhecidos:

f = 1,8 × 10 7 × 9,8 × sin ⁡ 24 ° = 7,2 × 10 7   N

Como f < f s m á x então o bloco não desliza.

Passo 5

A força mínima será aquela que supera o valor de f s m á x . Logo, reescrevendo a e q . 3 adicionando a força paralela ao plano A A ' :

f s m á x - P sin ⁡ θ - F = 0

Isolando F e substituindo os valores conhecidos:

F = 10 , 08 × 10 7 - 1,8 × 10 7 × 9,8 × sin ⁡ 24 ° = 2,9 × 10 7   N

Resposta

  1. N ã o   d e s l i z a ;
  2. F = 2,9 × 10 7   N .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco B da Fig. 6-31 pesa 711N . O coeficiente de atrito estático entre o bloco e a mesa é 0,25 ; o ângulo θ é 30 ° ; suponha que trecho da corda entre o bloco B e o nó é horizontal. Determine o pes
Uma caixa de areia, inicialmente estacionária, vai ser puxada em um piso por meio de um cabo no qual a tensão não deve exceder 1100N . O coeficiente de atrito estático entre a caixa e o piso é de 0,35
Os dois blocos ( m = 16k g e M = 88k g ) da Fig. 6-38 não estão ligados. O coeficiente de atrito estático entre os blocos é μ s = 0,38 , mas não há atrito na superfície abaixo do bloco maior. Qual é o
Por volta de 1915, Henry Sincosky, da Filadélfia, pendurou-se no caibro de um telhado apertando-o com os polegares de um lado e os outros dedos do outro lado (Fig. 6-21). A massa de Sincosky era 79k g
Na Fig. 6-49, uma alpinista de 49 kg está subindo por uma "chaminé". O coeficiente de atrito estático entre as botas e a pedra é 1,2 ; entre as costas e a pedra é 0,80 . A alpinista reduziu a força qu