Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 19

Uma caixa de areia, inicialmente estacionária, vai ser puxada em um piso por meio de um cabo no qual a tensão não deve exceder 1100   N . O coeficiente de atrito estático entre a caixa e o piso é de 0,35 . (a) Qual deve ser o ângulo entre o cabo e a horizontal para que se consiga puxar a maior quantidade possível de areia e (b) qual é o peso da areia e da caixa nesta situação?

Passo 1

Para começar esta questão, vamos fazer um DCL para ilustrar melhor as forças que atuam na caixa de areia:

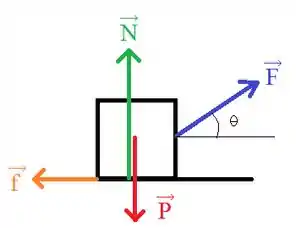
A partir da ilustração conseguimos aplicar a segunda lei de Newton para cada eixo:

e i x o   x :         F x - f a t = m a x       e q . 1

e i x o   y :         N + F y - P = m a y       e q . 2

Vamos analisar eixo por eixo.

Passo 2

No eixo x como estamos querendo o ângulo para puxar a maior quantidade de areia possível, então devemos pensar na mínima força que devemos aplicar para fazer com que a caixa de areia se mova. Assim, devemos considerar a força de atrito estático máximo e, portanto, a x = 0 . Reescrevendo a e q . 1 :

F cos ⁡ θ - μ s N = 0

Substituindo os valores conhecidos e isolando N :

N = 1100 cos ⁡ θ 0,35       e q . 3

Passo 3

Vamos fazer de maneira análoga para o eixo y . Lembrando que o movimento deve ocorrer somente na horizontal e, portanto, a y = 0 :

N + F sin ⁡ θ - m g = 0

Substituindo os valores conhecidos e isolando N :

N = m × 9,8 - 1100 sin ⁡ θ       e q . 4

Passo 4

Igualando a e q . 3 e a e q . 4 :

1100 cos ⁡ θ 0,35 = m × 9,8 - 1100 sin ⁡ θ

Como queremos o ângulo para mover a maior massa possível, então vamos isolar m :

m = 1100 × cos ⁡ θ 0,35 + sin ⁡ θ 9,8       e q . 5

Para determinar o ângulo pedido, podemos derivar a massa em função de θ e analisar o ponto crítico:

d m d θ = - sin ⁡ θ 0,35 + cos ⁡ θ × 1100 9,8

Lembrando que por definição um ponto crítico é o ponto onde a derivada não existe ou é zero. Neste nosso caso, vamos buscar o ponto que a derivada é zero, no qual para ser zero o que está dentro do parênteses tem que ser zero, show? Então vamos igualar isso a zero:

- sin ⁡ θ 0,35 + cos ⁡ θ = 0

cos ⁡ θ = sin ⁡ θ 0,35

sin ⁡ θ cos ⁡ θ = tan ⁡ θ = 0,35

Isolando o θ :

θ = tan - 1 ⁡ 0,35 = 19,3 °

Portanto o ângulo que a corda deve fazer com a horizontal para puxar a maior massa possível é θ = 19,3 ° .

Passo 5

Para determinar qual o valor dessa massa usaremos a e q . 5 substituindo o valor do ângulo θ calculado no passo anterior. Assim:

m = 1100 9,8 × cos ⁡ 19,3 ° 0,35 + sin ⁡ 19,3 ° = 339,8   k g

Para determinar o peso:

P = m g = 339,8 × 9,8 = 3330   N

Resposta

  1. θ = 19,3 ° ;
  2. P = 3,3   k N .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro está viajando a 50,0m i / h em uma rodovia horizontal. Se o coeficiente de atrito estático entre a estrada e os pneus em um dia chuvoso é 0,100 , qual é a distância mínima em que o carro para
A pessoa na Figura P5.6 pesa 170l b . Como visto de frente, cada muleta faz um ângulo de 22,0 ° com a vertical. Metade do peso da pessoa é suportada pelas muletas. A outra é suportada pelas forças ver
Antes de 1960, as pessoas acreditavam que o coeficiente de atrito estático máximo atingível para um pneu de automóvel em uma rodovia era μ S=1 . Por volta de 1962, três empresas desenvolveram, de form
Um bloco de 3,00k g é empurrado contra uma parede por uma força P → que forma um ângulo θ=50,0 ° com a horizontal, como mostra a Figura P5.12. O coeficiente de atrito estático entre o bloco e a parede
Por que a seguinte situação é impossível? Uma torradeira de 1,30k g não está ligada na tomada. O coeficiente de atrito estático entre ela e uma bancada horizontal é 0,350 . Para fazer a torradeira com