Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 10
Por volta de 1915, Henry Sincosky, da Filadélfia, pendurou-se no caibro de um telhado apertando-o com os polegares de um lado e os outros dedos do outro lado (Fig. 6-21). A massa de Sincosky era . Se o coeficiente de atrito estático entre as mãos e o caibro era , qual foi, no mínimo, o módulo da força normal exercida sobre o caibro pelos polegares ou os dedos do lado oposto? (Depois de se pendurar, Sincosky ergueu o corpo e deslocou-se ao longo do caibro, trocando de mão . Se você não dá valor ao feito de Sincosky, tente repetir a proeza.)
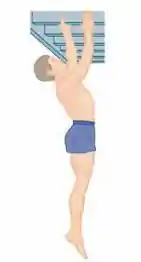
Passo 1
Então galera , nós sabemos que , como não há aceleração , a soma das forças de atrito estático (que são quatro, uma para cada polegar e uma para cada conjunto dos outros quatro dedos) é igual à força da gravidade. Assim , temos que :
Que , para , nos dá
Resposta
Atenção! Cientistas afirmam que o próximo exercício tem 117,3% de chances de cair na sua prova , não deixem de conferir J