Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.4 - Ex. 3

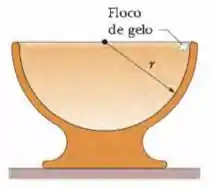
Na Fig. 8-30, um floco de gelo de 2,00   g é liberado na borda de uma taça hemisférica com 22,0   c m de raio. Não há atrito no contato do floco com a taça. (a) Qual é o trabalho realizado sobre o floco pela força gravitacional durante a descida do floco até o fundo da taça? (b) Qual é a variação da energia potencial do sistema floco-Terra durante a descida? (c) Se essa energia potencial é tomada como nula no fundo da taça, qual é seu valor quando o floco é solto? (d) Se, em vez disso, a energia potencial é tomada como nula no ponto onde o floco é solto, qual é o seu valor quando o floco atinge o fundo da taça? (e) Se a massa do floco fosse duplicada, os valores das respostas dos itens (a) e (d) aumentariam, diminuiriam ou permaneceriam os mesmos?

Passo 1

  1. Oi, galerinha! Tudo bom? Para resolver essa questão temos que lembrar que a força gravitacional é uma força consertativa, então podemos calcular o trabalho realizado por esta força usando o seguinte teorema:

    2. W g = - ∆ U g

    Assim, escrevendo a equação da energia potencial gravitacional, temos:

    W g = - m g ∆ y

    Portanto, podemos perceber que o trabalho só depende da variação de altura. Para esta questão, vamos considerar que nosso y = 0 seja o ponto mais baixo da taça.

    Lembrando que usaremos um fator multiplicativo de 10 - 2 no raio da taça para transformar de c m para m , e um fator também multiplicativo de 10 - 3 na massa para transformar de g para k g .

    Passo 2

    Analisando o ponto inicial e o ponto que o gelo atinge o ponto mais baixo, a variação de altura é:

    ∆ y = 0 - 22 × 10 - 2 m

    Assim:

    W g = m g ∆ y

    W g = - 2 × 10 - 3 × 9,8 × - 22 × 10 - 2

    W g = 4,31 × 10 - 3   J

    Passo 3

  2. Temos pela fórmula da energia potencial, que quanto menor a altura, ∆ y , menor a energia potencial. Se estamos observando um movimento de descida, a energia potencia será negativa.

    3. Deste modo, a negativa da energia potencial já foi calculada no passo anterior para determinar o trabalho, então:

    ∆ U g = - W g = - 4,31 × 10 - 3   J

    Passo 4

  3. Considerando, ainda, o fundo da taça como y = 0 , então a energia potencial quando o gelo é solto é:

    4. U g = m g R

    U g = 2 × 10 - 3 × 9,8 × 22 × 10 - 2

    U g = 4,31 × 10 - 3   J

    Passo 5

  4. Considerando, agora, o ponto de onde o gelo foi solto como y = 0 , então a energia potencial quando ele alcança a parte mais baixa da taça é:

    5. U g = m g - R

    U g = 2 × 10 - 3 × 9,8 × - 22 × 10 - 2

    U g = - 4,31 × 10 - 3   J

    Passo 6

  5. Devemos perceber que todas as equações usadas nesta questão são proporcionais a massa do gelo, portanto, se a massa do gelo fosse multiplicada por dois, todas as respostas seriam duplicadas também.

Resposta

  1. W g = 4,31 × 10 - 3   J ;
  2. ∆ U g = - 4,31 × 10 - 3   J ;
  3. U g = 4,31 × 10 - 3   J ;
  4. U g = - 4,31 × 10 - 3   J ;
  5. T o d a s   a s   r e s p o s t a s   d u p l i c a r i a m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 8-32 mostra uma haste fina, de comprimento L = 2,00m e massa desprezível, que pode girar em torno de uma das extremidades para descrever uma circunferência vertical. Uma bola de massa m = 5,00k
A Fig. 8-29 mostra uma bola de massa m = 0,341k g presa à extremidade de uma haste fina de comprimento L = 0,452m e massa desprezível. A outra extremidade da haste é articulada, de modo que a bola pod
Na Fig. 8-31, um pequeno bloco de massa m = 0,032k g pode deslizar em uma pista sem atrito que forma um loop de raio R = 12c m . O bloco é liberado a partir do repouso no ponto P , a uma altura h = 5,
Você está em uma roda gigante que gira com rapidez constante. Certo ou errado: Durante qualquer fração de uma revolução: (a) Nenhuma das forças atuando sobre você realiza trabalho sobre você. (b) O tr