Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.4 - Ex. 14
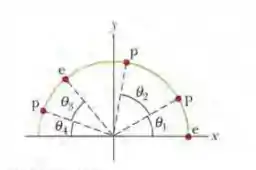
A Fig. 22-37 mostra um arranjo irregular de elétrons (e) e prótons (p) em um arco de circunferência de raio , com ângulos , , e . Determine (a) o módulo e (b) a orientação (em relação ao semieixo positivo) do campo elétrico no centro do arco.
Passo 1
É isso ai galerinhaa do mal!!
Vamos começar mais umaa??
Nesse problema foi dado um sistema de partículas carregadas e nosso objetivo é calcular o modulo e a orientação do campo elétrico na origem do sistema!
Antes de qualquer coisa vamos lembrar como calculamos o campo elétrico para uma partícula?
Olha que legal, a distância é a mesma para todas as partículas e a carga dos prótons equivale a enquanto a dos elétrons,
Então se analisarmos o módulo do campo vamos obter:
Sacou? Bora começar! 😉
Passo 2
Primeiro vamos obter o módulo do campo elétrico...
Sabendo que:
Substituindo em vemos que cada campo que os prótons geram é dada por
Achamos o módulo, mas como o campo é um vetor precisamos lembrar que quando as cargas são negativas o campo aponta para a carga e quando a carga é positiva o campo aponta para bem longe dela, ok?
Já os campos gerados pelos elétrons são dados por de mesmo modulo, mas com sinais opostos
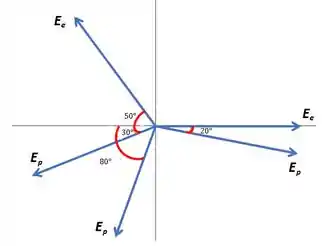
Vamos desenhar:
Tranquilo até aqui? 😁
Passo 3
Então nós teremos uma componente resultante do campo elétrico na direção x e outro na y, certo?
Para achar a letra (a) nós primeiro teremos que achar as duas componentes do campo resultante!
Vamos olhar? Vou seguir a ordem apresentada lá no enunciado, ok? Onde o primeiro representa 1, a próxima 2 e assim por diante:
Lembrando lá da trigonometria:
Para achar o módulo mais uma vez a matemática nos trás a solução:
A letra (a) tá terminada!! Bora pra (b)??
Passo 4
Se lembrarmos lá da nossa querida trigonometria, que vire e mexe vem nos salvar, vamos lembrar que a direção do campo pode ser dada por:
Finalizamos mais umaaa!!
Ihuuuuuul
Resposta
a)
b)