Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.4 - Ex. 11

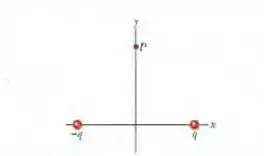
A Fig. 22-34 mostra duas partículas carregadas mantidas fixas no eixo x : - q =   - 3,20 · 10 - 19   C , no ponto x = -   3,00   m , e q = 3,20 · 10 - 19   C , no ponto x = + 3,00   m . Determine (a) o módulo e (b) a orientação (em relação ao semieixo x positivo) do campo elétrico no ponto P , para o qual y = 4,00   m .

Passo 1

Shooow galerinha, vamos para mais uma questão beeem legal!!

Nesse problema temos duas cargas - q = - 3,20 · 10 - 19   C em x = - 3 m e q = 3,20 · 10 - 19   C em x = 3 m .

A partir daí queremos calcular o campo elétrico no ponto P em y = 4 m .

Parece complicado? 🤔

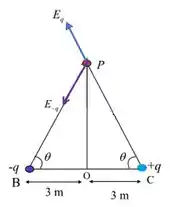
Antes de qualquer coisa nós vamos aplicar os campos que estão chegando lá no ponto P , ok? Na carga - q o campo é apostado para ela, enquanto para a + q o campo aponta para longe! Como a distância até a origem é a mesma, teremos o mesmo ângulo.

Agora é só desenhar:

Como as forças são angulares, elas terão componentes nas direções x e y:

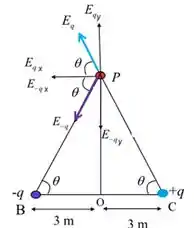
Bora começar! 😬

Passo 2

Bom, o campo elétrico é calculado por uma fórmula:

E = k q r 2

Se k é uma constante, o campo elétrico depende somente da carga e da distância entre elas e o ponto P. Então, o campo elétrico produzido por elas terá a mesma intensidade, porém direções diferentes, ocasionadas pelas cargas positivas e negativas.

Olhando na figura acima podemos concluir que:

E - q , y = E q , y

E - q , x = E q , x

Novamente no desenho nós vemos que o campo resultante será:

E R e s u l t a n t e , y = E q , y - E - q , y = E q , y - E q , y = 0

E R e s u l t a n t e , x = E q , x + E - q , x = E q , x + E q , x = 2 E q , x

Isso aqui já responde a letra (b), certo? Nós temos um campo resultante sendo apontado na direção negativa de x !!

E agora nós podemos seguir para a letra (a)!!

Veja só! 😁

Passo 3

Bom, se lembrarmos da trigonometria da coisa:

E q , x = E . cos ⁡ θ

Então:

E R e s u l t a n t e , x = 2 E . cos ⁡ θ

Substituindo o campo:

E R e s u l t a n t e , x = 2 . k q r 2 cos ⁡ θ

E o que nós temos aqui? Quase nada: q = 3,20 · 10 - 19   C e k = 8,99 · 10 9 N m 2 C 2

Nós precisamos de r e do cosseno, certo?

O r   é a hipotenusa do triângulo retângulo formado entre uma das cargas e o ponto P , e é calculada como:

r 2 = 4   m 2 + 3   m 2 = 25   m 2

r = 5   m

O cosseno também é possível calcular olhando este mesmo triângulo:

cos ⁡ θ = C a t e t o   A d j a c e n t e H i p o t e n u s a = 3   m 5   m = 0,6

Agora sim!!

É só colocar na fórmula:

E R e s u l t a n t e , x = 2 . 3,20 · 10 - 19   C 8,99 · 10 9 N m 2 C 2 25   m 2 0,6

E R e s u l t a n t e , x = 1,38 · 10 - 10 N C

Chegamos ao fim de mais umaa!!

Entendeu tudo? Responde Aí! 😉

Resposta

a)   E x =   1,38 · 10 - 10   N / C

b) O campo elétrico aponta no sentido negativo de x .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas cargas são colocadas como indica a Figura 21.53 . O módulo de q 1 é igual a 3,0μ C , porém não conhecemos seu sinal e nem o valor da carga q 2 . O campo elétrico resultante E → no ponto P aponta
Trace de forma esquemática as linhas de força associadas a um par de cargas puntiformes de + 2 q e - q , separadas por uma distância d . Explique o traçado e discuta qualitativamente o comportamento d
Um modelo clássico de uma molécula ionizada é constituído por um par de partículas fixas, ambas de carga + e , separadas por uma distância 2 a , com uma terceira partícula, de carga - e , massa m , de
Há um campo elétrico uniforme na região entre duas placas planas paralelas com cargas de sinais contrários. Um próton é liberado do repouso na superfície da placa com carga positiva e, depois de um in
Determine o módulo, a direção e o sentido (em relação ao eixo +O x ) do campo elétrico no exemplo 21.6.Uma carga puntiforme de - 2,5n C é colocada no ponto P da figura 21. 19. Determine o módulo, a di