Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 22.4 - Ex. 14
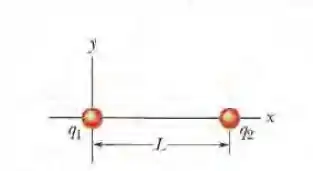
Na Fig. abaixo, a partícula 1, de carga = - 5,00q, e a partícula 2, de carga = +2,00q, são mantidas fixas no eixo x. (a) E que ponto do eixo, em termos da distância L, o campo elétrico total é nulo? (b) Faça um esboço das linhas de campo elétrico.
Passo 1
O enunciado nos dá uma configuração de duas partículas de cargas com sinais opostos e ele quer saber em que ponto do eixo x teremos o campo elétrico resultante dessas duas partículas nulo e pede para fazermos o esboço das linhas de campo elétrico.
Primeira coisa que devemos saber é que as linhas do campo elétrico de uma carga positiva apontam para fora:
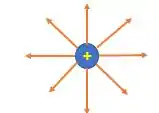
Enquanto cargas negativas geram linhas de campo elétrico que apontam pra dentro:
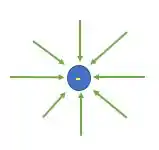
Logo, o campo produzido por elas é como na figura:
As setas azuis representam o campo produzido pela carga 1 (negativa) e as vermelho o campo produzido pela carga 2 (positiva).
No meio das cargas os campos se somam, então não há como se anularem nesse espaço.
Já à direita da carga 2 e à esquerda da carga 1 os campos possuem sentidos contrários, então o campo resultante pode se anular nesse espaço, belezinha?
Passo 2
O módulo da carga é maior que a . Portanto, o ponto que procuramos tem que ser mais longe da partícula 1 do que da partícula 2, para que o campo tenha o mesmo módulo e se cancele, isto acontece à direita da partícula 2.
Usando a fórmula de cálculo de campo elétrico devido a uma partícula pontual, chamaremos de a coordenada do ponto em que o campo elétrico é nulo:
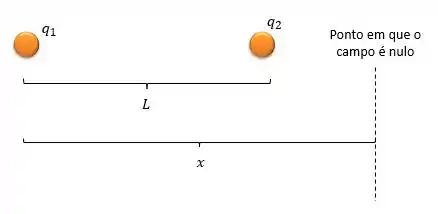
O módulo do campo elétrico devido às partículas deve ser igual para o campo elétrico total ser nulo.
Se o campo gerado por uma carga é:
O campo gerado pela carga 1 será:
Enquanto o campo gerado pela carga 2 será:
Logo, para eles se anularem:
Substituindo os valores para e para achar , temos:
Cortamos os dois de cada lado:
Assim como cortamos o valor de :
Aplicando a raíz quadrada dos dois lados:
Como a coordenada é à direita da partícula 2, o tem que ser positivo, então:
Passo 3
Item (b)
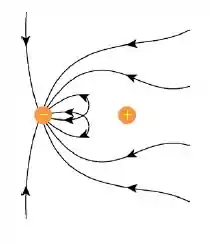
Fizemos o esboço das linhas de campo elétrico, note que há maior densidade de linhas próximo a partícula 1, pois ela tem módulo maior:
