Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.5 - Ex. 15

Na Fig. 28-34, um paralelepípedo metálico de dimensões d x = 5,00 m , d y = 3,00 m e d z = 2,00 m está se movendo com velocidade constante v → = 20,0 m / s i ^ em uma região onde existe um campo magnético uniforme B → = 30,0 m T j ^ . Determine (a) o campo elétrico no interior do objeto, em termos dos vetores unitários; (b) a diferença de potencial entre as extremidades do objeto.

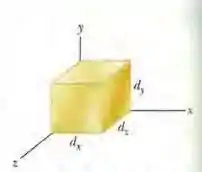
Passo 1

E aí, tudo certinho? 😁

Neste exercício temos um paralelepípedo que está se movendo em uma região onde existe um campo magnético temos que determinar o campo elétrico no interior a diferença de potencial nas extremidades do objeto.

Tem ideia de como fazemos isso? 👀

Para obter o campo elétrico, fazemos

E → = v B →

Sabendo que E → aponta para o sentido oposto de v → × B →

Já para obter o potencial, fazemos

V = E d

Veja só! 😉

Passo 2

(a) Estamos interessados em calcular o campo eletrostático que é estabelecido quando

as cargas se separam por ação do campo magnético. Uma vez estabelecido o equilíbrio, a

Eq. 28-10 nos dá

E → = v B → = 20,0 m / s × 0,03 T

E → = 0,6 V / m .

Se v → aponta na direção i ^ e B → na direção j ^ , vamos obter que v → × B → = - k ^ .

Dessa forma, temos que

E → = - 0,6 V / m k ^

Tranquilo até aqui? 😊

Passo 3

(b) Temos que o campo magnético está na direção j ^ e a velocidade do bloco na direção i ^ , então o campo elétrico estará na direção da força magnética, ou seja, na direção do produto vetorial

v ^ × B ^ = i ^ × j ^ = k ^

Então nessa direção vai haver uma diferença de potencial que é dada por

V = E d z

E estamos usando a distância d z por que é nessa direção que está o campo elétrico. Assim vamos ter

V = E d z = 0,6 × 2

V = 1,2   V

Belezinha? Responde Aí! 😁

Resposta

a) E → = - 0,6 V / m k ^

b) V = 1,2   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Imagine que na sala em que você está sentado exista um campo magnético uniforme B apontando verticalmente para baixo. No centro da sala, dois elétrons são projetados, de repente, com a mesma velocidad
Um elétron descreve uma trajetória helicoidal em um campo magnético uniforme de módulo 0,300 T. O passo da hélice é 6,00 μ m e o módulo da força magnética experimentada pelo elétron é 2,00 × 10 - 15N
Um dipolo magnético com um momento dipolar de módulo 0,020J / T é liberado a partir do repouso em um campo magnético uniforme de módulo 52 m T e gira livremente sob a ação da força magnética. Quando o
Uma certa partícula subatômica decai em um elétron e um pósitron. Suponha que, no instante do decaimento, a partícula está em repouso em um campo magnético uniforme B → de módulo 3,53 m T e que as tra
Uma linha de transmissão horizontal é percorrida por uma corrente de 5000A no sentido sul-norte. O campo magnético da Terra ( 60,0 μ T ) tem a direçāo norte e faz um ângulo de 70 , 0 ∘ c o m a horizon