Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.9 - Ex. 48
Uma bobina de uma espira, percorrida por uma corrente de 4,00 A, tem a forma de um triângulo retângulo cujos lados medem , e . A bobina é submetida a um campo magnético uniforme de módulo paralelo à corrente no lado de . Determine o módulo da força magnética (a) no lado de ; (b) no lado de ; (c) no lado de . (d) Determine a força total que o campo magnético exerce sobre a espira.
Passo 1
E aí, galerinha! 😎
Temos uma espira em forma de triângulo retângulo com corrente , com os lados de tamanhos 50, 120 e 130 cm. Além disso, é aplicado um campo magnético uniforme na mesma direção do lado que mede 130 cm e mesmo sentido da corrente. Podemos visualizar o esquema pela figura:
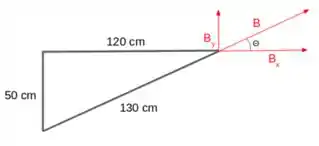
Dessa, forma, podemos achar o ângulo :
Com isso, o campo magnético em cada direção é:
Veja só! 😁
Passo 2
(a) Temos a seguinte equação:
Como a direção do fio é a mesma do campo, a força é zero já que o produto vetorial entre dois vetores de mesmo sentido é nulo.
Tranquilo até aqui? 😉
Passo 3
(b) Nesse caso, temos que a componente perpendicular ao fio exerce a força no fio, portanto:
Substituindo os valores dados no enunciado, chegamos em.
Bacana, não é? 😇
Passo 4
(C) Temos então:
Substituindo os valores dados no enunciado...
Estamos quase lá! 😁
Passo 5
(d) a força dos itens (b) e (c) apontam na mesma direção. Porém, como uma é componente e a outra é , temos que sua soma é:
Portanto, a força total é zero.
E aí! entendeu tudo? Responde Aí! 😎
Resposta
(a) (b)(c)
(d)