Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 27
A figura 12-38 mostra sua mão segurando um florete, a arma usada na prática da esgrima. O centro de massa do florete está a do botão (a extremidade do florete na empenhadura). Você pesou o florete e sabe que sua massa é e que seu comprimento total é . (a) No início da luta, você segura o florete apontando para a frente, em equilíbrio estático. Determine a força total exercida pela sua mão sobre o florete. (b) Determine o torque exercido pela sua mão sobre o florete. (c) Sua mão, sendo um corpo com extensão, na verdade exerce uma força distribuída sobre a empunhadura do florete. Adote um modelo em que a força total exercida pela sua mão é representada por duas forças opostas, cujas linhas de ação estão separadas pela largura da sua mão (considere ). Determine as magnitudes e as orientações destas duas forças.
Passo 1
Olha aí a representação da situação, já considerando a letra (c) que fala que a força da mão vai ser dividida em duas forças opostas separadas de .
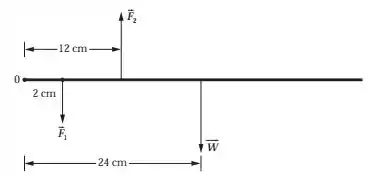
Passo 2
- Se a força total que nossa mão exerce no florete é , podemos fazer equilíbrio das forças na vertical, já que o florete está em equilíbrio.
- Para o florete ficar em equilíbrio, o somatório dos torques sobre ele tem que ser nulo! Mas só tem a mão e o peso fazendo torque, e então o torque da mão tem que ser igual ao torque do peso!
- Aqui é só a gente fazer a mesma coisa, considerando a distância entre as duas forças!
Passo 3
Passo 4
Equilíbrio na vertical, considerando a força da esquerda para baixo e a força da direita para cima:
Equilíbrio de momento em relação ao final do florete:
Resolvendo esse sistema, vamos obter: